文章信息
- 姜烈, 何江涛, 许真, 刘玉梅
- JIANG Lie, HE Jiang-tao, XU Zhen, LIU Yu-mei
- 硝酸盐污染地下水原位碳源注入生物修复优化方案研究
- Optimization of In-Situ Carbon Injection Bioremediation of Nitrate Contaminated Groundwater
- 农业环境科学学报, 2014, 33(10): 2014-2021
- Journal of Agro-Environment Science, 2014, 33(10): 2014-2021
- http://dx.doi.org/10.11654/jaes.2014.10.019
-
文章历史
- 收稿日期:2014-6-16
2. 江西省地质环境监测总站, 南昌 330012
2. Jiangxi Geological Environment Monitoring Station, Nanchang 330012, China
硝酸盐是一种普遍存在的地下水污染物。人类的工农业生产、农业用肥、垃圾渗滤液、含氮工业废水的渗漏、化粪池渗漏、污水的回灌等都会不同程度地引起地下水中硝酸盐氮浓度的上升,其中垃圾渗滤液和生活污水的影响也较为突出。过量的硝酸盐对人体非常不利,容易使婴儿患上高铁血红蛋白症,俗称蓝婴病[1].世界卫生组织、欧盟和美国规定,地下水中硝酸盐氮含量不应超过10 mg·L-1[2].因此治理地下水硝酸盐污染刻不容缓。
目前硝酸盐污染地下水修复技术主要有两种:原位生物修复技术和抽出处理技术。从去除地下水中硝酸盐污染和降低治理成本这两个方面看,原位生物修复技术是目前已投入实用的最经济、最有效的方法[3].硝酸盐原位生物修复技术的原理实际上是通过注入井添加碳源,刺激反硝化细菌的生长,从而强化硝酸盐污染物的自然生物降解过程。
生物降解作用可以通过一级动力学方程或者Monod方程来耦合到对流-弥散方程。耦合的生物降解模型用来模拟多种有机物的生物降解,也可以用来模拟地下水中硝酸盐生物降解。将碳源注入受硝酸盐污染的地下水,强化微生物反硝化,建立溶质模型模拟原位反硝化试验[4,5].在实际运用中,由于碳源类型和不同修复方案的限制,使得数值模型在设计和评估原位修复技术中发挥重要作用[6].然而这些生物降解模型只是单纯模拟有机物的生物降解过程,并没有体现原位生物修复系统优化管理目标、约束条件以及优化技术。原位生物修复技术优化的核心在于如何通过合理的井数注入适量的碳源使得治理成本最小。通常考虑的因素包括注入碳源井位置、注入碳源井数、注入碳源量、碳源注入成本和碳源注入设备成本。在优化的过程中将生物降解模型与优化模型进行耦合,从而使原位生物治理成本最小化。 运用到地下水修复系统的各种优化技术方法包括线性规划、非线性规划、二次规划、最优控制算法、动态规划和整数规划,然而这些方法在优化过程中容易陷入局部优化[7,8].为了解决此类问题,近年来发展迅速的有遗传算法、模拟退火法等全局优化方法。
将遗传算法和模拟退火法模型的优点和局限性与线性规划、非线性规划以及微分动态规划的结果相对比,证明遗传算法和模拟退火法在优化成本方面能够实现全局优化[9].Huang 等[10]使用遗传算法优化地下水修复系统设计,在优化模型中,以抽水量及抽水井位置和注入量及注入井的位置作为决策变量,结果表明动态的抽水速率和井的位置比之前的研究效果更好,能够节省成本,具有全局优化地下水修复方案的能力。Hsiao等[11]结合遗传算法解决了井的安装成本、固定成本和目标函数总费用地下水管理问题,得出最优治理方案。Sinha 等[12]提出多尺度注射遗传算法优化,包括不同空间尺度的适应度函数,用来减少抽出修复优化问题的计算时间。彭伟等[13]将水流模型(MODFLOW)和水质模型(MT3DMS)耦合,采用Pareto 遗传算法进行求解,同时开发应用程序NPGA-GW并运用于二维地下水污染修复问题的多目标优化求解。全局优化算法的优点在于能够避免局部优化,找到全局最优点或最优解。
与此类似,优化模型也被运用于地下水生物修复管理。Rizzo 等[14]利用模拟退火法对下水修复问题进行优化设计。在约束条件下,对目标函数进行优化,目的是获得修复井随时间的最佳位置。同时对成本函数包含安装成本、运行成本和注入成本及开采井的维护成本等进行优化。遗传算法相比大量的“试错法”而言,有能力降低地下水修复的计算成本。说明遗传算法在地下水修复优化设计中能够体现其优化的特点[15].Shieh 等[7]在地下水原位生物修复设计中,利用模拟退火法对目标函数总成本最小化进行优化,优化最佳井数、井位置及注入量和抽出速率。表明模拟退火法在地下水修复寻找全局最优解方面具有优点。
本文以北京某场地生活垃圾填埋场硝酸盐污染地下水为研究对象,针对原位生物修复技术,利用RT3D模块建立双重Monod动力学反应,模拟电子供体碳源和电子受体硝酸盐同时被反硝化细菌利用。在双重Monod动力学反应模拟基础上,利用遗传算法和模拟退火法对研究布置的18口井进行原位修复模拟优化,使原位生物修复效果达标且治理成本最小化。同时优化最佳井位置、井数及碳源注入量。 1 材料和方法 1.1 RT3D原理
地下水中垃圾渗滤液中的硝酸盐迁移转化是综合物理、化学及生物作用的过程,其中包括对流与扩散、吸附与解吸、衰减及生物降解过程等。
Visual MODFLOW中的Reactive Transport in Three-Dimensions(RT3D)能够进行地下水溶质运移模拟,最早由Dr. Clement开发出一个一维有限差分(1DCART),用来研究土柱的脱氮过程。1995年Dr. Clement修改了运算法则,把1DCART 模型移植到MT3D模型中,这就形成了最初的RT3D,后来Dr. Clement总结了多种反应模型,编辑形成了一个新的多相反应程序--RT3D.2000年RT3D成功植入到MT3DMS中。经过10多年的发展,RT3D已经成为最有影响力的模拟计算多组反应的三维运移模型,特别是在模拟有机物的自然衰减和生物修复方面具有很大的优势[16].
采用对流-弥散方程描述污染物在地下水中的运移,即:
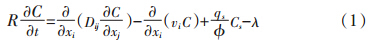
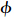 准表示地层介质的孔隙度,无量纲;t表示时间,d;R表示阻滞因子,无量纲;x表示运移的距离,m;v表示渗透速度,m·d-1;D-弥散系数,m2·d-1;qs表示单位体积含水层源汇通量,d-1;Cs表示源或汇的浓度,mg·L-1;λ表示液相中化学反应总和,mg·L-1·d-1.
1.2 双重Monod生物反应
准表示地层介质的孔隙度,无量纲;t表示时间,d;R表示阻滞因子,无量纲;x表示运移的距离,m;v表示渗透速度,m·d-1;D-弥散系数,m2·d-1;qs表示单位体积含水层源汇通量,d-1;Cs表示源或汇的浓度,mg·L-1;λ表示液相中化学反应总和,mg·L-1·d-1.
1.2 双重Monod生物反应反硝化菌在缺氧的环境中,利用碳源作为电子供体,NO-3作为电子受体进行反硝化反应。因此,在反硝化过程中,NO-3和有机物两者均作为反硝化菌的基质被同时利用,其反应动力学可用双重Monod模式描述。其他抑制或促进反硝化因素,例如pH、温度、氧气等可以忽略不计[17].因此在MODFLOW内置模块RT3D中选择反应项Double-Monod degradation model.
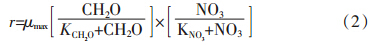
在地下水饱和带中将上述反硝化动力学反应(2)与溶质运移方程(1)进行耦合,得到如下方程:
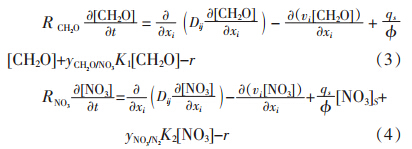
本论文研究中,有机碳源的利用速率和反硝化细菌生长速率可以描述成:

遗传算法(Genetic Algorithm)是一种通过模拟自然进化过程搜索最优解的方法。遗传算法的核心是选择、交叉、变异。它最初由美国Michigan大学J.Holland教授于1975年首先提出来的。遗传算法具有操作简单化、信息处理并行性、并行计算、扩展性等优点,从而能够成为一种被广泛应用于各种复杂系统优化方法。遗传算法提供了一种求解非线性、多模型、多参数、多目标等复杂系统优化问题的通用框架,已经被广泛地运用于函数优化、组合优化、机器人学、图形处理等领域。
模拟退火法(Simulated Annealing)是一种通用概率演算法,用来在一个大的搜寻空间内找寻命题的最优解。Metropolis等在1953年提出的Metropolis准则,1983年Kirkpatrick等受到Metropolis准则的启发,将退火思想引入组合优化问题,提出了模拟退火算法。模拟退火算法在某一较高初温条件下,结合具有概率突跳特性的Metropolis准则,在温度参数逐渐下降的过程中,在解空间中进行随机搜索,寻找目标函数的全局最优解[26].
在模拟优化过程当中,需要不断调用MODFLOW和RT3D程序来求解不同目标函数的值。从USGS官网下载MODFLOW 和RT3D源代码,在FORTRAN语言环境下,将MODFLOW和RT3D改写成为GA和SA的两个可以随时调用的C语言子程序,检查所有的状态变量(注入速率、水头和浓度)是否能够满足所有的约束条件。 1.4 地下水生物降解模型
在硝酸盐原位修复系统中,最主要的工作是优化目标函数,使得修复系统的总费用最小。目标函数主要包括优化井安装费用、碳源注入成本费用和碳源注入设备费用[27,28].

研究区位于北京某场地,所处区域地势平坦。场地东侧为养殖场,西南侧为当地居民耕作农田,农村垃圾和畜禽养殖废水均排放到池塘,见图 1.姜烈等[29]对研究场地信息有详细描述。

|
| 图 1 地下水硝酸盐初始污染羽分布图和备选井位置 Figure 1 Initial groundwater nitrate contamination plumes and potential well locations |
在研究区进行单孔抽水试验,通过Aquifer Test软件分析,得出含水层的平均渗透系数为3.37 m·d-1.研究区场地范围较小,可以将研究区假设为均质各向异性含水层。将场地概化成一层。研究场地为225 m×200 m,将其剖分成2.25 m×2 m.地下水从北东方向向南西方向流。研究区的初始水力坡度约为0.01.西北方向和东南方向为隔水边界。地下水硝酸盐的阻滞因子设为1.模型输入参数见表 3.
利用Geoprobe钻机对生活垃圾填埋场地下水及池塘污水进行取样调查。现场测试数据:池塘地表水的NH+4-N高达46.8 mg·L-1,同时地表 50 cm渗坑NO-3-N高达65 mg·L-1.研究区地下水硝酸盐仍处于不断变化的情况,同时场地调查尚不够充分,还不足以刻画出实际地下水硝酸盐的污染羽状体。因此,本研究以农村垃圾和畜禽养殖废水为污染源,硝酸盐氮入渗浓度为65 mg·L-1,模拟在天然地下水流动情况下释放5年形成的硝酸盐污染羽作为原位生物修复的初始污染羽。研究区硝酸盐氮初始污染羽总量为36.99 kg,见图 1. 2.3 原位修复备选井方案
为了设计合理的原位生物修复治理优化方案,根据模拟生成硝酸盐污染羽形成的范围及通过试错法确定较为有效的注入井位置,在研究区布置了18口备选井方案。研究区周围地下水硝酸盐氮背景浓度约为1 mg·L-1.将研究区红色框作为浓度约束区,在100 d内连续注入碳源,达到将研究区硝酸盐氮浓度降低到10 mg·L-1的目标。 3 讨论 3.1 最优适应度评估
GA设定的相关参数:种群大小为100;迭代次数为100;编码长度为6;交叉概率为0.9;变异系数为0.05;离散化区间数为32.SA设定的相关参数:初始温度为1,抽样次数10 000,降温率为0.9,最大迭代次数为100.在GA中使用适应度来衡量群体中各个个体在优化计算中能接近或有助于找到最优解的优良程度。一般而言,适应度高的个体遗传到下一代的概率就较大;而适应度较低的个体遗传到下一代的概率就相对较小。适应度函数总是正的,但目标函数有正有负,有时求最大值,有时求最小值,因此需要在目标函数和适应度函数之间进行转换。SA同理。
GA和SA优化算法在运行前期最优适应度变化很快,后期变化稍微缓慢,最后逐渐收敛,见图 2.

|
| 图 2 GA和SA最优适应度变化 Figure 2 Changes of GA and SA optimal fitness |
在原位修复量化时得到碳源浓度为50 mg·L-1时硝酸盐去除量较佳,因此本文选择碳源浓度为50 mg·L-1作为注入浓度。在100 d内连续注入浓度为50 mg·L-1的碳源,反硝化细菌为0.002 mg·L-1,GA和SA分别优化了碳源注入量、井的位置及井数,见图 3.GA和SA优化的井数和位置均相同,分别是井5、井7和井9.GA各井优化的碳源注入量分别为2.5 m3·d-1、1.5 m3·d-1和1.3 m3·d-1;SA优化各井碳源注入量分别为2.2 m3·d-1、1.4 m3·d-1和1.5 m3·d-1.

|
| 图 3 GA和SA优化井的注入速率及其井位置 Figure 3 Injection rates and well locations optimized by GA and SA methods |
在优化井中注入相应的碳源,GA和SA 优化80 d后硝酸盐污染羽,见图 4.GA和SA在优化80 d后,其硝酸盐氮最高浓度分别为13 mg·L-1和15 mg·L-1,井5、井7和井9附近硝酸盐被修复,形成硝酸盐净化带。注入碳源100 d后,两种优化方法都同时达到修复目的,即在100 d后研究区的硝酸盐氮都低于修复治理目标10 mg·L-1,见图 5.100 d后硝酸盐氮生物降解总去除量分别为33.58 kg和31.26 kg,其总量去除率分别为90.78%和84.51%.

|
| 图 4 GA和SA注入碳源80 d后地下水硝酸盐分布 Figure 4 Distribution of nitrate plumes in groundwater after 80 days of injecting carbon |

|
| 图 5 GA和SA注入碳源100 d后地下水硝酸盐分布 Figure 5 Distribution of nitrate plumes in groundwater after 100 days of injecting carbon |
在GA和SA优化三口井后注入相应碳源,构成灌注式PRBs原位修复。在灌注式PRBs内加入碳源,可以加强对地下水硝酸盐污染的去除,形成具有一定长度和宽度的硝酸盐净化带。国外研究和国内小规模的现场研究表明这种方法是行之有效的。利用三个井将碳源注入到含水层中,提高反硝化细菌的活性,能够达到去除硝酸盐的目的。 3.3 GA与SA对比分析
将GA和SA优化技术方法运用于原位生物修复系统,在满足各项约束条件下,从18口备选井方案中确定最佳井数、井的位置及其碳源注入量,使得原位生物修复系统总成本达到最小。GA和SA优化井数一样,所以两种优化方法井安装成本都是60 000元。GA的碳源注入成本和碳源注入设备成本要比SA的多,导致GA系统总成本要比SA的系统总成本高,见表 4.可以看出,在本研究中SA优化方法比GA优化方法体现出了一定的优越性,能够节省系统总成本。
图 6显示GA和SA系统总成本的比例分配情况。可以看出,两种情况下系统总成本分配情况非常相似。在修复总成本中,可以看出GA碳源注入设备成本和碳源注入成本分别只占总成本的27%和11%,而SA碳源注入设备成本和碳源注入成本分别只占总成本的26%和11%.GA和SA井安装成本分别占总成本的62%和63%.可以看出井的安装成本对总成本整体构成有重要影响。所以在碳源注入量较低的情况下,增加井数对最优方案而言并没有优势,反而会增加修复系统成本。两种优化方法都是三口注入井,且优化井的位置是相同的,但优化的碳源注入量不一样,使得系统治理成本有差别。两种优化算法对比表明SA治理成本要比GA节省1.46%.在最小化治理成本下,GA和SA全局优化井数、碳源注入量、安装成本、碳源注入设备成本,使得优化结果可信。

|
| 图 6 GA和SA系统总成本分布对比 Figure 6 Comparison of overall costs of systems optimized by GA and SA methods |
图 7显示了GA、SA遗传代数与目标函数优化收敛对比。GA在50代后优化目标函数趋于收敛,而SA在20代后趋于稳定,说明SA的收敛速度比GA的要强。GA在前30代目标函数优化波动性比SA要大。两者最终都趋于稳定。在模型运行时,SA计算时间要比GA的长。两种优化方法都能识别决策变量的最佳组合。

|
| 图 7 GA、SA目标函数优化收敛对比 Figure 7 Comparison of convergence of optimal objective functions by GA and SA methods |
(1)以北京某场地生活垃圾填埋场硝酸盐污染地下水为研究对象,建立生物耦合Monod溶质运移模型,利用遗传算法(GA)和模拟退火法(SA)对地下水硝酸盐污染羽治理区中布置18口备选井方案和原位生物修复系统进行模拟优化。GA优化井5、井7和井9的碳源注入量分别为2.5 m3·d-1、1.5 m3·d-1和1.3 m3·d-1;SA优化井5、井7和井9碳源注入量分别为2.2 m3·d-1、1.4 m3·d-1和1.5 m3·d-1.反硝化细菌降解硝酸盐氮总量去除率分别为90.78%和84.51%.
(2)优化结果说明注入井的布置方式呈三角点布置,且上游点的碳源注入量大于其他两点注入量。地下水硝酸盐原位生物修复两种优化算法对比表明SA优化系统治理成本比GA节省1.46%,且收敛性强,波动性小,但计算时间较长。原位生物修复系统优化模拟可为实现场地修复地下水中硝酸盐污染科学管理和有效治理提供技术支撑。
致谢:本研究场地基础信息调查由中国环境科学院、北京建工环境修复有限责任公司、轻工环保研究所等人共同完成,在此一并表示感谢。
| [1] | Haugen K, Semmens M, Novak P. A novel in situ technology for the treatment of nitrate contaminated groundwater[J]. Water Research, 2002, 36(14):3497- 3506. |
| [2] | Sadeq M, Moe C L, Attarassi B, et al. Drinking water nitrate and prevalence of methemoglobinemia among infants and children aged 1-7 years in Moroccan areas[J]. International Journal of Hygiene and Environmental Health, 2008, 211(5):546-554. |
| [3] | 王振兴, 李向全, 侯新伟, 等. 地下水硝酸盐污染的生物修复技术研究进展[J]. 环境科学与技术, 2012, 1:163-166. WANG Zhen-xing, LI Xiang-quan, HOU Xin-wei, et al. The research progress and status of bioremediation of nitrate pollution of groundwater[J]. Environmental Science & Technology, 2012, 1:163-166. |
| [4] | Lee M S, Lee K K, Hyun Y, et al. Nitrogen transformation and transport modeling in groundwater aquifers[J]. Ecological Modelling, 2006, 192(1):143-159. |
| [5] | Eljamal O, Jinno K, Hosokawa T. Modeling of solute transport with bioremediation processes using sawdust as a Matrix[J]. Water, Air, and Soil Pollution, 2008, 195(1-4):115-127. |
| [6] | Prommer H, Tuxen N, Bjerg P L. Fringe-controlled natural attenuation of phenoxy acids in a landfill plume:Integration of field-scale processes by reactive transport modeling[J]. Environmental Science & Technology, 2006, 40(15):4732-4738. |
| [7] | Shieh H J, Peralta R C. Optimal in situ bioremediation design by hybrid genetic algorithm-simulated annealing[J]. Journal of Water Resources Planning and Management, 2005, 131(1):67-78. |
| [8] | Yoon J H, Shoemaker C A. Improved real-coded GA for groundwater bioremediation[J]. Journal of Computing in Civil Engineering, 2001, 15(3):224-231. |
| [9] | Wang M, Zheng C. Ground water management optimization using genetic algorithms and simulated annealing:Formulation and comparison[J]. Journal of the American Water Resources Association, 1998, 34(3):519-530. |
| [10] | Huang C, Mayer A S. Pump-and-treat optimization using well locations and pumping rates as decision variables[J]. Water Resources Research, 1997, 33 (5):1001-1012. |
| [11] | Hsiao C T, Chang L C. Dynamic optimal groundwater management with inclusion of fixed costs[J]. Journal of Water Resources Planning and Management, 2002, 128(1):57-65. |
| [12] | Sinha E, Minsker B S. Multiscale island injection genetic algorithms for groundwater remediation[J]. Advances in Water Resources, 2007, 30(9):1933-1942. |
| [13] | 彭 伟, 吴剑锋, 吴吉春. NPGA-GW 在地下水系统多目标优化管理中的应用[J]. 高校地质学报, 2008, 14(4):631-636. PENG Wei, WU Jian-feng, WU Ji-chun. Application of niched pareto genetic algorithm to multi-objective optimal design of groundwater system[J]. Geological Journal of China Universities, 2008, 14(4):631-636. |
| [14] | Rizzo D M, Dougherty D E. Design optimization for multiple management period groundwater remediation[J]. Water Resources Research, 1996, 32(8):2549- 2561. |
| [15] | Espinoza F P, Minsker B S. Goldberg D E. Adaptive hybrid genetic algorithm for groundwater remediation design[J]. Journal of Water Resources Planning and Management, 2005, 131(1):14-24. |
| [16] | 宁立波, 董少刚, 马传明. 地下水数值模拟的理论与实践[M]. 武汉:中国地质大学出版社, 2010:25-26. NING Li-bo, DONG Shao-gang, MA Chuan-ming. The theory and practice of groundwater numerical simulation[M]. Wuhan:China University of Geosciences press, 2010:25-26. |
| [17] | Killingstad M W, Widdowson M A, Smith R L. Modeling enhanced in situ denitrification in groundwater[J]. Journal of Environmental Engineering, 2002, 128(6 ):491-504. |
| [18] | Kinzelbach W, Schäfer W, Herzer J. Numerical modeling of natural and enhanced denitrification processes in aquifers[J]. Water Resources Research, 1991, 27(6):1123-1135. |
| [19] | Clement T, Peyton B, Skeen R, et al. Microbial growth and transport in porous media under denitrification conditions:Experiments and simulations[J]. Journal of Contaminant Hydrology, 1997, 24(3):269-285. |
| [20] | Baek N, Clesceri L, Clesceri N. Modeling of enhanced biodegradation in unsaturated soil zone[J]. Journal of Environmental Engineering, 1989, 115(1):150 -172. |
| [21] | Kornaros M, Lyberatos G. Kinetic modelling of pseudomonas denitrificans growth and denitrification under aerobic, anoxic and transient operating conditions[J]. Water research, 1998, 32(6):1912-1922. |
| [22] | Essaid H I, Bekins B A, Godsy E M, et al. Simulation of aerobic and anaerobic biodegradation processes at a crude oil spill site[J]. Water Resources Research, 1995, 31(12):3309-3327. |
| [23] | Henze M, Grady Jr C, Gujer W, et al. A general model for single-sludge wastewater treatment systems[J]. Water Research, 1987, 21(5):505-515. |
| [24] | 王丽丽, 赵 林, 谭 欣, 等. 不同碳源及其碳氮比对反硝化过程的影响[J]. 环境保护科学, 2004, 30(1):15-18. WANG Li-li, ZHAO Lin, Tan Xin, et al. Influence of different carbon source and ratio of carbon and nitrogen for water denitrification[J]. Environmental Protection Science, 2004, 30(1):15-18. |
| [25] | 许保玖, 龙腾锐. 当代给水与废水处理原理[M]. 高等教育出版社, 2000:402-533. XU Bao-jiu, LONG Teng-rui. Contemporary principles of water and wastewater treatment[M]. Higher Education Press, 2000:402-533. |
| [26] | 江思珉, 朱国荣, 胡西嘉, 等. 单纯形-模拟退火混合算法反求水文地质参数及其并行求解[J]. 地质论评, 2007, 53(1):92-97. JIANG Si-min, ZHU Guo-rong, HU Xi-jia, et al. Hybrid simplex-simulated annealing method for solving hydrogeologic parameters and its parallel implementation[J]. Geological Review, 2007, 53(1):92-97. |
| [27] | Hemker T, Fowler K R, Farthing M W, et al. A mixed-integer simulation-based optimization approach with surrogate functions in water resources management[J]. Optimization and Engineering, 2008, 9(4):341-360. |
| [28] | Schaerlaekens J, Mertens J, Van Linden J, et al. A multi-objective optimization framework for surfactant-enhanced remediation of DNAPL contaminations[J]. Journal of contaminant hydrology, 2006, 86(3):176-194. |
| [29] | 姜 烈, 何江涛, 姜永海, 等. 地下水硝酸盐污染抽出处理优化方法模拟研究[J]. 环境科学, 2014, 35(7):2573-2577. JIANG Lie, HE Jiang-tao, JIANG Yong-hai, et al. Simulation of nitrate pollution in groundwater using pump-and-treat optimization method[J]. Environmental Science, 2014, 35(7):2573-2577. |
 2014, Vol. 33
2014, Vol. 33