快速检索        
  农业环境科学学报  2017, Vol. 36 Issue (10): 2153-2160

文章信息

韩术鑫, 王利红, 赵长盛
HAN Shu-xin, WANG Li-hong, ZHAO Chang-sheng
内梅罗指数法在环境质量评价中的适用性与修正原则
Applicability and modifications of the Nemerow index method in evaluating environmental quality
农业环境科学学报, 2017, 36(10): 2153-2160
Journal of Agro-Environment Science, 2017, 36(10): 2153-2160
http://dx.doi.org/10.11654/jaes.2017-0519

文章历史

收稿日期: 2017-04-10
 Abstract              PDF               Figures               Tables
引用本文 0
韩术鑫, 王利红, 赵长盛. 内梅罗指数法在环境质量评价中的适用性与修正原则[J]. 农业环境科学学报, 2017, 36(10): 2153-2160. DOI: 10.11654/jaes.2017-0519.
HAN Shu-xin, WANG Li-hong, ZHAO Chang-sheng. Applicability and modifications of the Nemerow index method in evaluating environmental quality[J]. Journal of Agro-Environment Science, 2017, 36(10): 2153-2160. DOI: 10.11654/jaes.2017-0519.
内梅罗指数法在环境质量评价中的适用性与修正原则
韩术鑫 , 王利红 , 赵长盛     
山东省分析测试中心, 济南 250014
收稿日期: 2017-04-10
基金项目: 山东省重点研发计划（2015GSF120010）
作者简介: 韩术鑫(1984-), 男, 山东诸城人, 助理研究员, 主要研究方向为环境监测与环境质量评价。E-mail:hsxaa369@qq.com
摘要: 为研究内梅罗指数法在环境要素质量评价中的适用性及确定其修正原则，将方法的计算公式进行了数学推导。结果表明：典型内梅罗指数法的计算公式可变换为线性表达式，其斜率和截距分别为最大值（Fj，max）和算术平均值（Fj，ave）的权重系数；随着Fj，max与Fj，ave比值的增大，Fj，max权重增大，Fj，ave权重减小。参评污染因子数量（n）对方法的评分结果具有重要影响，典型内梅罗指数法更适用于区域中目的性和指向性较明确或总体污染程度较轻的环境要素质量评价。为提高方法的适用性，确定了2种修正内梅罗指数法的划分原则，Ⅰ型和Ⅱ型修正内梅罗指数法分别以n和Fj，max/Fj，ave等于5作为划分结点，其中：Ⅰ型修正内梅罗指数法倾向于参评因子不多、评价目的性和指向性较强的环境要素质量评价；Ⅱ型修正内梅罗指数法是对Ⅰ型修正内梅罗指数法的拓展和延伸，更适用于多因子综合性质量评价。由内梅罗指数法线性表达式的数学内涵可知，在n或Fj，max/Fj，ave ≤ 5时，方法可不作修正，此时并不影响评价结果的客观性和准确性。
关键词: 内梅罗指数法     环境要素     方法适用性     方法修正原则     污染因子权重    
Applicability and modifications of the Nemerow index method in evaluating environmental quality
HAN Shu-xin, WANG Li-hong, ZHAO Chang-sheng     
Shandong Analysis and Test Center, Ji'nan 250014, China
Project supported: The Key Technology Research and Development Program of Shandong Province, China (2015GSF120010)
Abstract: In order to study the applicability and modifications of the Nemerow index(NI) method used for evaluations of environmental quality, mathematical derivations were performed based on the original formula. The results showed that the formula of the NI method could be transformed into a linear equation. The slope and intercept of the equation could be the weight coefficients of the maximum value(Fj, max) and arithmetic mean value(Fj, ave), respectively. With increases in the ratio of Fj, max to Fj, ave, the weight of Fj, max increased while that of Fj, ave decreased. The number of pollution factors(n) participating in the evaluation had a significant influence on the results. The NI method was found to be more suitable for evaluation of environmental factors with clear purposes and directions, or those associated with low pollution in a region. In order to improve the applicability of the NI method, some modifications were proposed for two revised Nemerow index(RNI) methods. For the Ⅰ-RNI method, n=5 was used as the partition node, and the ratio of Fj, max to Fj, ave was equal to five for the Ⅱ-RNI method. The Ⅰ-RNI method was used to evaluate factors with clear purposes and directions, and those associated with less pollution; the Ⅱ-RNI method, an extension of the Ⅰ-RNI method, was more suitable for multifactor comprehensive evaluation. Based on the mathematical connotation of the linear equation for the NI method, when n or the ratio of Fj, max to Fj, ave is not more than 5, the original NI method can be used without affecting the objectivity and accuracy of the evaluation results.
Key words: Nemerow index method     environmental factors     applicability of methods     modifications of methods     weights of pollution factors    

内梅罗指数法由单因子指数法发展而来，是当前国内外进行综合污染指数计算最常用的方法之一。该方法是一种兼顾极值或突出最大值的计权型多因子环境质量指数[1]，能够较全面地反映各种污染物的协同作用，从而较准确地评价各类环境要素的污染程度。该方法最早由美国雪城大学（Syracuse University）内梅罗（N.L. Nemerow）教授在其所著的《河流污染科学分析》一书中提出。自20世纪70年代以来，被我国一些环保科研人员应用于某些地区的水污染评价中[2]。发展至今，该方法在近岸海域海水[2-5]、河流[6-10]、湖泊[11-12]、湿地水环境[13-14]、饮用水源地水环境[15-16]、地下水[17-26]等水质类环境质量评价，以及河道沉积物[27]、海洋沉积物[28-30]、土壤[1, 31-38]等环境要素中重金属、有机氯、多氯联苯、多环芳烃等高毒高危害性污染物的环境健康风险评价中均作为重要的评价方法广泛应用，倍受科研工作者的青睐。

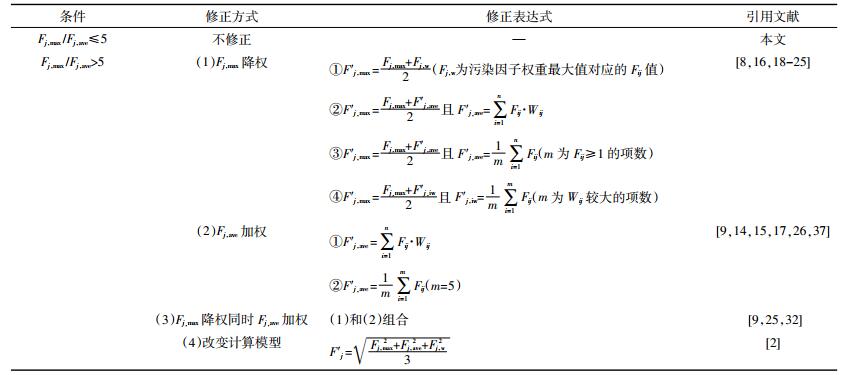
内梅罗指数法具有计算过程简洁、物理概念清晰、可操作性强等优点[18]，但在实际应用过程中出现了一些问题，导致评价结果有时不能准确真实地反映所评价的环境要素质量。主要体现在如下几个方面：（1）评价时只考虑了单因子污染指数算术平均值和最大值，且最大值权重过高[8, 16, 18-25]；（2）未考虑参评污染因子的毒性、危害性在评价的环境要素中的权重[9, 14, 15, 25-26, 32, 37]；（3）未揭示参评污染因子种类和数量对评价值的影响。针对以上问题，许多科研人员通过各种途径和方法对内梅罗指数进行改进或修正，取得了一定的成效，但并未从根本上讲清楚该方法应用于环境要素的适用性问题以及进行修正的原则划分。本文通过对典型内梅罗指数法计算公式的数学推导，探讨了该方法的数学原理，并以此为依据深入分析了其在环境要素质量评价中的适用性。另外，划分了该方法修正与否的基本原则，为科研人员和环保决策部门开展环境质量评价提供实用性较强的操作方法。

1 材料与方法 1.1 典型内梅罗指数法

典型内梅罗指数法包含单因子污染指数的算术平均值和最大值，单因子污染指数法和内梅罗指数法的计算公式分别如下：

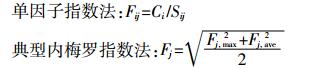
式中：Fj为按某环境要素质量标准中第j种标准计算得出的评分值；Fj, max为在某环境要素质量标准第j种标准下Fij的最大值，Fj, max =max{Fij}；Fj, ave为在某环境要素质量标准第j种标准下Fij的算术平均值，Fj, ave=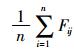；i为参评污染因子数量，i=1，2，…，n；j为某环境要素质量标准选取的污染因子所对应的质量类别，j=1，2，…，m；Ci为第i种污染因子的实测浓度；Sij为第i种污染因子在某环境要素质量标准中第j种标准下的标准值。

1.2 基于方法修正引入的不同环境要素中污染因子权重的计算

引入污染因子权重是对典型内梅罗指数法进行修正的重大突破，因环境要素的特点不同，污染因子权重的计算方式略有不同。

1.2.1 水质类污染因子权重的计算

由于各类污染物对人体与环境的毒性与危害程度存在较大的差异性，一般地，某种污染因子的危害性与该污染因子的排放标准基本上呈反比例的内在关系[39]。具体计算过程如下：首先以环境要素质量标准为依据，确定评价标准级别j；其次，将j类标准等级下各种参评污染因子的排放标准Si按由小到大顺序排列S1，S2，…，Sn，将其最大值Smax与Si比较，令Ri表示第i种污染因子的相关性比值，可得：

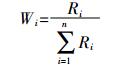
式中：Wi为第i种污染因子的权重值，（Ri =Smax/Si），。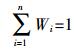

1.2.2 沉积物和土壤中污染因子权重的计算

开展地表水、地下水等环境要素的质量评价时，一般参评的污染因子较多且类别分散，评价结果更倾向于综合性；而针对土壤和沉积物的质量评价主要针对特定的某类污染因子（如重金属、多环芳烃等），具有更明显的指向性。因此，其污染因子的权重计算方式差异较大。关于重金属污染因子权重的计算，简要介绍几种方式：

第一种权重和类别依据Swaine提出的环境影响程度划分[40]，把Hg、Pb、Cd、As、Cr、Se几种毒性较高的元素归为Ⅰ类，Mn、Mo、V、Be、Th、U、Ni、Zn、Cu几种毒性较低的元素归为Ⅱ类，Ⅰ类和Ⅱ类分别设权重为3和2[37]。其他重金属元素如Co、Ba、Ra、Sb、Sn、Ti等划归Ⅲ类。

第二种权重的计算通过徐争启等[41]应用潜在生态危害指数法（RI），依据Hakanson的计算原则并结合陈静生[42]的计算方法，得到12种重金属元素的毒性系数（表 1）。

表 1 基于RI法确定的12种重金属毒性系数 Table 1 The toxicity coefficients of 12 heavy metals based on RI method
表选项

第三种依据林丽钦[43]研究的基于毒理学安全评价数据推算出重金属毒性系数，17种重金属的规正化权重见表 2。

表 2 基于毒理学确定的17种重金属规正化权重 Table 2 The toxicity coefficients of 17 heavy metals based on toxicology
表选项

第四种计算方法是李雪梅等[44]基于改进的层次分析法（AHP法），以重金属污染物在粮食中的限量值为依据，确定了7种重金属污染因子的权重系数（表 3）。

表 3 基于改进AHP法确定的7种重金属污染因子权重系数 Table 3 The toxicity coefficients of 7 heavy metals based on revised AHP method
表选项

另外，邹乔等[32]通过多元线性回归的方式计算出16种多环芳烃浓度权重，具体见表 4。

表 4 基于多元线性回归确定的16种多环芳烃污染因子权重系数 Table 4 The toxicity coefficients of 16 PAHs based on multiple linear regression
表选项
2 结果与讨论 2.1 典型内梅罗指数法计算公式的线性推导及方法适用性分析

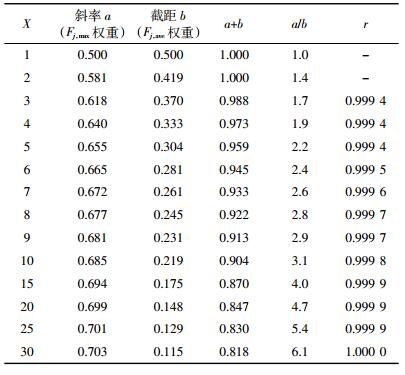
典型内梅罗指数法的计算公式等于单因子污染指数的最大值和算术平均值平方和一半的几何平均，在原公式的框架内，对参数Fj、Fj, max和Fj, ave的相关性分析较为困难。因此，本文对3个参数进行了技术性变换：令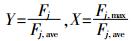，经线性拟合可得Y=aX+b，见图 1。将Y与X分别用上述变换式带入公式后可得：Fj =aFj, max+bFj, ave。通过线性推导可知内梅罗指数值实际上是单因子污染指数最大值和算术平均值加权后的和，斜率a和截距b分别代表的是Fj, max和Fj, ave的权重系数。

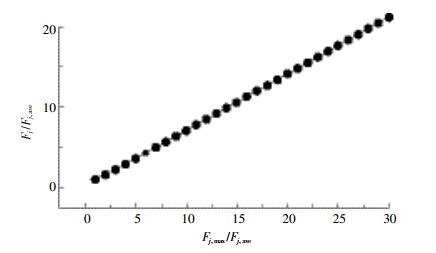
图 1 Fj/Fj，ave与Fj，max/Fj，ave的线性关系图 Figure 1 Linear relation between Fj/Fj, ave and Fj, max/Fj, ave
图选项

表 5是X取不同值时斜率a、截距b和线性相关性r的相应数值。由表 5可知：随着X的增加，Fj, max权重系数a逐渐增大，Fj, ave权重系数b逐渐减小，权重系数之和不断减小，权重系数之比逐渐增大。这说明单因子污染指数的最大值与算术平均值之比越大，则Fj, max的权重系数就越大，Fj, ave的权重系数越小，Fj, max在Fj中的作用越突出。更为重要的是，随着Fj, max与Fj, ave比值的增大，权重系数之和与理论权重系数之和1.00的差距不断扩大，显示Fj在某类环境要素质量评价的代表性逐步下降，因为存在一项权重系数为[1-（a+b）]的未知参数没有参与Fj的计算。根据Fj, ave与Fj, max之间的关系可知：[Fj, max/n]≤Fj, ave≤Fj, max（n指参评的污染因子的数量），则1≤[Fj, max/Fj, ave]≤n，即1≤X≤n。这说明参评的污染因子数量n实际上对典型内梅罗指数法的评分值Fj存在着重要影响。n越大，则出现Fj, max权重系数过大，Fj, ave权重系数过小的风险越高。由于未知参数的权重系数随着X的增加而不断增大，其对Fj的贡献越来越不可忽视，由表 5可知：当X≥20时，未知参数的权重系数甚至超过了Fj, ave的权重系数，所以仅以Fj, max和Fj, ave两项参数参与Fj的计算将导致最终的评价结果可信度降低，适用性下降。

表 5 典型内梅罗指数法线性推导相关参数一览表 Table 5 Parameters of linear derivation based on typical NI method
表选项

典型内梅罗指数法的线性推导从数学基本原理的角度反映了其内部存在的问题实际上是受多种因素共同影响的，除了Fj, max和Fj, ave外，n的作用往往被评价者所忽略。基于以上问题的讨论，为了达到准确客观的评价结果，有必要对典型内梅罗指数法在环境要素中的适用性进行严谨的分析。为便于进行分析，将[1-（a+b）]称为未知项权重系数c。由表 5可分析，导致典型内梅罗指数法出现适用性问题的根本原因是c值对应的未知参数未参与到Fj的计算中，只要解决了这个问题即可从根本上消除内梅罗指数法的不足。由于准确推导未知参数的数学表达式不具可操作性，本研究从相反的角度着手，即尽可能地降低c值，使得未知参数在整个Fj的计算过程中的贡献值可忽略不计，从而确保最终评价结果客观、可信。

由表 5可知：当n=5、10、20、30时，c值分别为0.041、0.096、0.153、0.182。所以，要维持典型内梅罗指数法的适应性可从2个途径进行构建：第一，针对某类环境要素质量评价的目的和意义，合理选择参评因子种类和数量，选择有典型代表性的几项污染因子。例如针对土壤中重金属的环境风险评价，一般选择Hg、Pb、Cd、As、Ni、Zn、Cr、Cu这8种重金属，为了提高方法适用性可进一步根据重金属毒性高低筛选出Hg、Pb、Cd、As、Cr这5项作为参评污染因子。其他的环境要素可依此类推。因此，从该角度可知，典型内梅罗指数法更适用于目的性和指向性较明确的环境要素质量评价；第二，不限制参评污染因子数量，从控制Fj, max与Fj, ave的比值着手，二者的比值越小，方法的适用性越高。对于未受污染或污染极重的环境要素评价，二者的比值虽然较小但评价结果无法分级，是没有实际意义的。因此，从反向推论可得典型内梅罗指数法适用于某个区域中污染程度较轻的环境要素的质量评价，这与一些学者的研究结论相吻合[13]。

2.2 典型内梅罗指数法修正原则的划分

在实际环境要素质量评价过程中，出现了典型内梅罗指数法适用性不强的情况，将导致评价结果不够客观公正，说服力不足。许多科研工作者通过多种途径对该方法进行改进或修正，提高了方法适用性，获得了较为真实客观可信的评价结果。但典型内梅罗指数法应该采用怎样的修正原则，缺乏系统地、科学地分析。为此，我们以该法数学推导得到的线性方程式为依据，结合方法适应性的基本原则，详细探讨典型内梅罗指数法的修正原则。

修正的根本目的是扩大方法的适用性，提高评价结果的准确性。从上文可知，典型内梅罗指数法存在2个主要的适用性限制。首先，基于第一种适用性分析，从参评污染因子数量的角度确定如下修正原则，并命名为Ⅰ型修正内梅罗指数法（表 6）。从表 5可知，有5个参评的污染因子时，出现的极端情况是X=5，此时对应的Fj, max与Fj, ave的权重之和为0.959，权重之比2.2，算术平均值的权重大于0.3，最大值的作用未出现过分突出的情况，且未知项的权重很低，对总评分的贡献可以忽略，典型内梅罗指数法可以不作修正即可保证评价结果的可靠性。因此，为了既突出最大值的作用又使算术平均值在总评分值中的贡献适当，选定n等于5作为修正划分的结点[17]。以此为界限划分出条件（1）和条件（2）。在条件（2）中再以X等于5为结点，划分成条件（2-1）和（2-2）。值得注意的是，当出现条件（2-2）时，为了提高Fj, ave对Fj的贡献，防止Fj, max作用过分突出，以及控制未知项的权重c，令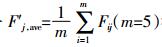替代原先值，即选择n项参评污染因子中最有代表性的5项重新计算出F′j，ave。其筛选过程其实是另一种形式的加权过程，筛选原则可以根据不同污染因子的毒性高低（表 1~表 4）或者人体对污染因子的敏感程度进行。该修正方式使得Fj, max与F′j，ave的比值重新拉回到不修正的条件范围内，从而满足了典型内梅罗指数法的适用性原则。Ⅰ型修正内梅罗指数法的修正策略更加倾向于参评因子不多、评价目的性和指向性较强的环境要素质量评价，在上述情况下，更容易从全部参评因子中选择出能代表此次评价结果的污染因子。例如，环境要素中某些特定类别的污染物（重金属、多环芳烃等）的环境污染风险评价可以用该方法予以修正。

表 6 Ⅰ型修正内梅罗指数法的修正原则 Table 6 Modifications of Ⅰ-RNI method
表选项

基于上述分析，注重环境要素多方位多层次多参评因子的综合性质量评价不适用于Ⅰ型修正内梅罗指数法。为此，诸多研究人员打破典型内梅罗指数法的固有计算方式，通过增加污染因子权重的方式，对Fj, max降权和（或）对Fj, ave加权的方式，得到Ⅱ型修正内梅罗指数法（表 7）。这种修正方式相当于在原来方法的基础上引入1项或几项新的参数，参与Fj的计算。由表 7可知：Ⅱ型修正内梅罗指数法不限制参评污染因子数量，主要以Fj, max /Fj, ave作为修正的必要条件。如上所述，当该比值不大于5时，典型内梅罗指数法具有适用性，故不作修正；比值大于5时，相关学者采用了从4种不同的修正方式对方法进行了修正。其中针对Fj, max降权的修正方式又包含4类修正表达式，特别是修正表达式① 在实际应用中最为常见。降权的总体思路是引入参评污染因子中权重最大的1项或者几项的评分值与Fj, max进行算术平均，使其权重降低一半，另一半权重赋予污染因子权重较高的评分值，避免了Fj, max过高引起的Fj评分失真的情况。将Fj, ave加权有2种修正表达式：一种由算术平均值修正为加权平均值，另一种是Ⅰ型修正内梅罗指数法采用的选择有代表性的5项污染因子参与Fj, ave的计算，2种不同形式的加权均增加了污染因子权重对Fj的贡献，使结果更加全面客观地反映环境要素的质量状况。将Fj, max降权和Fj, ave加权结合起来则双向增加了污染因子权重对Fj的影响。以上3种修正方式都基于内梅罗指数法的计算公式框架不变的前提下进行。杨琳[2]则突破了原先的计算模型，将污染因子权重最大值对应的Fj，w直接作为第三项参数，Fj为Fj, max、Fj, ave和Fj，w3项的几何平均值。总体而言，Ⅱ型修正内梅罗指数法是对典型内梅罗指数法的大胆突破和创新，较大地扩展了方法的适用性，提高了评价结果的客观性和准确性。对于参评污染因子众多的环境要素的综合性质量评价，修正意义尤其重大。同时，该法也是对Ⅰ型修正内梅罗指数法的拓展和延伸，对于评价指向性和目的性较强的环境要素质量评价同样适用。

表 7 Ⅱ型修正内梅罗指数法的修正原则 Table 7 Modifications of Ⅱ-RNI method
表选项
3 结论

（1）经数学推导，典型内梅罗指数法计算公式可变换为线性表达式：Fj =aFj, max+bFj, ave。其中，斜率a和截距b分别代表单因子污染指数最大值（Fj, max）和算术平均值（Fj, ave）的权重系数。a和b的大小受Fj, max与Fj, ave比值的影响显著，随着比值的增大，Fj, max权重增大，Fj, ave权重减小。参评污染因子数量（n）对典型内梅罗指数法的评分结果存在着重要影响，n越大，典型内梅罗指数法对环境要素质量评价不适用的风险越高。

（2）典型内梅罗指数法更适用于区域中目的性和指向性较明确或者总体污染程度较轻的环境要素质量评价。

（3）为提高典型内梅罗指数法的适用性和评价结果的准确性，确定了2种修正内梅罗指数法的划分原则。Ⅰ型修正内梅罗指数法以n等于5作为划分结点，设置了1种修正方式，该法更加倾向于参评因子不多、评价目的性和指向性较强的环境要素质量评价，如环境要素中某类特定类别的污染物（重金属、多环芳烃等）的环境污染风险评价；Ⅱ型修正内梅罗指数法是对Ⅰ型修正内梅罗指数法的拓展和延伸，以Fj, max与Fj, ave比值等于5为划分结点，修正方式包括Fj, max降权、Fj, ave加权、Fj, max降权同时Fj, ave加权以及改变计算模型等4种，对多因子综合性质量评价更具适用性。

（4）在n≤5或Fj, max /Fj, ave≤5时，典型内梅罗指数法可不修正，不影响评价结果的客观性和准确性。

参考文献
[1]
陈京都, 戴其根, 许学宏, 等. 江苏省典型区农田土壤及小麦中重金属含量与评价[J]. 生态学报, 2012, 32(11): 3487-3496.
CHEN Jing-du, DAI Qi-gen, XU Xue-hong, et al. Heavy metal contents and evaluation of farmland soil and wheat in typical area of Jiangsu Province[J]. Acta Ecologica Sinica, 2012, 32(11): 3487-3496.
[2]
杨琳. 应用权重修正内梅罗污染指数法对陆源入海排污口邻近海域水环境质量综合评价[J]. 福建水产, 2010(2): 50-54.
YANG Lin. A comprehensive evaluation on coastal waters near pollutant discharge outlet with weighting-factor modified Nemerow index method[J]. Journal of Fujian Fisheries, 2010(2): 50-54.
[3]
丁菁. 内梅罗污染指数法在排污口邻近海域水环境质量评价中的应用[J]. 福建水产, 2016(1): 1-4.
DING Jing. An application of the Nemerow pollution index in the quality assessment of the seawater environment in the vicinity of terrestrial drains[J]. Journal of Fujian Fisheries, 2016(1): 1-4.
[4]
罗万次, 苏搏, 刘熊, 等. 北仑河口附近海域冬季海洋环境质量评价[J]. 广西科学院学报, 2014, 30(2): 107-111, 119.
LUO Wan-ci, SU Bo, LIU Xiong, et al. Winter marine environment quality assessment around the Beilun estuary[J]. Journal of Guangxi Academy of Sciences, 2014, 30(2): 107-111, 119.
[5]
宋永刚, 吴金浩, 邵泽伟, 等. 辽东湾近岸表层海水重金属污染分析与评价[J]. 渔业科学进展, 2016, 37(3): 14-19.
SONG Yong-gang, WU Jin-hao, SHAO Ze-wei, et al. Evaluation of heavy metal pollution in the offshore surface seawater of the Liaodong Bay[J]. Progress in Fishery Sciences, 2016, 37(3): 14-19. DOI:10.11758/yykxjz.20150820001
[6]
Yi Q, Dou X D, Huang Q R, et al. Pollution characteristics of Pb, Zn, As, Cd in the Bijiang River[J]. Procedia Environmental Sciences, 2012, 13(13): 43-52.
[7]
梁德华, 蒋火华. 河流水质综合评价方法的统一和改进[J]. 中国环境监测, 2002, 18(2): 63-66.
LIANG De-hua, JIANG Huo-hua. Unifying and improving the comprehensive assessment methods of river water quality[J]. Environmental Monitoring in China, 2002, 18(2): 63-66.
[8]
蔡晔, 林怡雯, 李月娥, 等. 利用改进的内梅罗指数法模型评价苏州市内外城河水质[J]. 化学分析计量, 2015, 24(2): 84-87.
CAI Ye, LIN Yi-wen, LI Yue-e, et al. Evaluation of water quality of city river in Suzhou by improved Nemerow index method[J]. Chemical Analysis and Meterage, 2015, 24(2): 84-87.
[9]
李小丽, 黎小东, 敖天其. 改进内梅罗指数法在西充河水质评价中的应用[J]. 人民黄河, 2016, 38(8): 65-68.
LI Xiao-li, LI Xiao-dong, AO Tian-qi. Application of improved Nemerow index method used in water quality assessment[J]. Yellow River, 2016, 38(8): 65-68.
[10]
郑利杰, 高红杰, 宋永会, 等. 我国典型城市地表水水质综合评价与分析[J]. 环境工程技术学报, 2016, 6(3): 252-258.
ZHENG Li-jie, GAO Hong-jie, SONG Yong-hui, et al. Comprehensive evaluation and analysis of surface water quality for typical cities of China[J]. Journal of Environmental Engineering Technology, 2016, 6(3): 252-258.
[11]
周笑白, 张宁红, 张咏, 等. 太湖水质与水生生物健康的关联性初探[J]. 环境科学, 2014, 35(1): 271-278.
ZHOU Xiao-bai, ZHANG Ning-hong, ZHANG Yong, et al. Preliminary study on the relationship between the water quality and the aquatic biological health status of Taihu Lake[J]. Environmental Science, 2014, 35(1): 271-278.
[12]
蔡晓强, 高强立. 基于内梅罗指数法评价开封市湖泊水质污染特征[J]. 吉林农业, 2016(11): 82-83.
CAI Xiao-qiang, GAO Qiang-li. Pollution characteristics of water quality in Kaifeng based on Nemerow index method[J]. Jilin Agriculture, 2016(11): 82-83.
[13]
孙清展, 臧淑英, 张囡囡, 等. 基于蒙特卡罗方法的扎龙湿地水环境质量评价[J]. 湿地科学, 2013, 11(1): 75-81.
SUN Qing-zhan, ZANG Shu-ying, ZHANG Nan-nan, et al. Evaluation of water environment quality of Zhalong wetlands based on Monte Carlo method[J]. Wetland Science, 2013, 11(1): 75-81.
[14]
吕俊芳, 王书锦, 刘云根, 等. 罗时江河口湿地水质季节变化特征及评价[J]. 环境工程, 2016(S1): 845-849, 877.
LÜ Jun-fang, WANG Shu-jin, LIU Yun-gen, et al. Seasonal variation characteristics of water quality and evaluation at the estuarine wetland of Luoshijiang River[J]. Environmental Engineering, 2016(S1): 845-849, 877.
[15]
何增辉. 修正内梅罗污染指数法在水源地环境质量评价中的应用[J]. 广东化工, 2011, 38(7): 141-143.
HE Zeng-hui. Application of improved Nemerow exponent method for evaluation of environmental quality of waterhead area[J]. Guangdong Chemical Engineering, 2011, 38(7): 141-143.
[16]
丁雪卿. 改进的内梅罗污染指数法在集中式饮用水源地环境质量评价中的应用[J]. 四川环境, 2010, 29(2): 47-51.
DING Xue-qing. Application of improved Nemerow index method for evaluation of environmental quality of waterhead area of public drinking water supply[J]. Sichuan Environment, 2010, 29(2): 47-51.
[17]
寇文杰, 林健, 陈忠荣, 等. 内梅罗指数法在水质评价中存在问题及修正[J]. 南水北调与水利科技, 2012, 10(4): 39-41, 47.
KOU Wen-jie, LIN Jian, CHEN Zhong-rong, et al. Existing problems and modifications of using Nemerow index method in water quality assessment[J]. South-to-North Water Diversion and Water Science & Technology, 2012, 10(4): 39-41, 47.
[18]
谷朝君, 潘颖, 潘明杰. 内梅罗指数法在地下水水质评价中的应用及存在问题[J]. 环境保护科学, 2002, 28(1): 45-47.
GU Zhao-jun, PAN Ying, PAN Ming-jie. The application and existed problems of Nemero index in groundwater quality evaluation[J]. Environmental Protection Science, 2002, 28(1): 45-47.
[19]
马成有, 曹剑锋, 姜纪沂, 等. 改进的内梅罗污染指数法及其应用——以磐石市地下水环境质量评价为例[J]. 水资源保护, 2006, 22(4): 53-55.
MA Cheng-you, CAO Jian-feng, JIANG Ji-yi, et al. Application of improved Nemerow index method to evaluation of groundwater quality in Panshi City[J]. Water Resources Protection, 2006, 22(4): 53-55.
[20]
关云鹏. 利用内梅罗指数法模型评价地下水水质的探讨[J]. 山西水利科技, 2012(1): 81-84.
GUAN Yun-peng. A discussion on evaluating groundwater quality by Nemerow index method[J]. Shanxi Hydrotechnics, 2012(1): 81-84.
[21]
张安昌, 庄付磊, 申铜飞, 等. 改进内梅罗指数法在聊城市地下水水质评价中的应用[J]. 治淮, 2016(12): 81-83.
ZHANG An-chang, ZHUANG Fu-lei, SHEN Tong-fei, et al. Application of improved Nemerow index method to evaluation of groundwater quality in Liaocheng City[J]. Zhihuai, 2016(12): 81-83. DOI:10.3969/j.issn.1001-9243.2016.12.051
[22]
于福荣, 卢文喜, 卞玉梅, 等. 改进的尼梅罗污染指数法在黄龙工业园水质评价中的应用[J]. 世界地质, 2008, 27(1): 59-62.
YU Fu-rong, LU Wen-xi, BIAN Yu-mei, et al. Application of improved Nemerow index method in evaluation of water quality in Huanglong industrial park catchment[J]. Global Geology, 2008, 27(1): 59-62.
[23]
李亚松, 张兆吉, 费宇红, 等. 内梅罗指数评价法的修正及其应用[J]. 水资源保护, 2009, 25(6): 48-50.
LI Ya-song, ZHANG Zhao-ji, FEI Yu-hong, et al. Improvement of Nemerow index method and its application[J]. Water Resources Protection, 2009, 25(6): 48-50.
[24]
Jie C, Qing L, Hui Q. Application of improved Nemerow index method based on entropy weight for groundwater quality evaluation[J]. International Journal of Environmental Sciences, 2012, 2(3): 1284-1290.
[25]
李玲玲. 内梅罗指数法的修正及应用[J]. 地下水, 2015, 37(5): 101-102, 107.
LI Ling-ling. Improvement and application of Nemerow index method[J]. Groundwater, 2015, 37(5): 101-102, 107.
[26]
闫欣荣. 修正的内梅罗指数法及其在城市地下饮用水源地水质评价中的应用[J]. 地下水, 2010, 32(1): 6-7.
YAN Xin-rong. Modified Nemerow exponent and application of the water quality evaluation in urban underground drinking water source area[J]. Groundwater, 2010, 32(1): 6-7.
[27]
章熙锋, 唐家良, 薛菲, 等. 5·12汶川大地震后涪江绵阳段沉积物重金属污染评价[J]. 环境保护科学, 2015, 41(5): 142-146.
ZHANG Xi-feng, TANG Jia-liang, XUE Fei, et al. Evaluation of heavy metal pollution in the sediments from Mianyang section of Fu River after the earthquake in Wenchuan on May 12[J]. Environmental Protection Science, 2015, 41(5): 142-146.
[28]
郑懿珉, 高茂生, 刘森, 等. 莱州湾表层沉积物重金属分布特征及生态环境评价[J]. 海洋环境科学, 2015, 34(3): 354-360.
ZHENG Yi-min, GAO Mao-sheng, LIU Sen, et al. Distribution patterns and ecological assessment on heavy metals in the surface sediments of Laizhou Bay[J]. Marine Environmental Science, 2015, 34(3): 354-360.
[29]
Brady J P, Ayoko G A, Martens W N, et al. Enrichment, distribution and sources of heavy metals in the sediments of Deception Bay, Queensland, Australia[J]. Marine Pollution Bulletin, 2014, 81(1): 248-255. DOI:10.1016/j.marpolbul.2014.01.031
[30]
Liu S, Zhang Y, Bi S, et al. Heavy metals distribution and environmental quality assessment for sediments off the southern coast of the Shandong Peninsula, China[J]. Marine Pollution Bulletin, 2015, 100(1): 483-488. DOI:10.1016/j.marpolbul.2015.09.028
[31]
Kowalska J, Mazurek R, Gąsiorek M, et al. Soil pollution indices conditioned by medieval metallurgical activity:A case study from Krakow(Poland)[J]. Environmental Pollution, 2016, 218: 1023-1036. DOI:10.1016/j.envpol.2016.08.053
[32]
邹乔, 王瑶, 杜显元, 等. 内梅罗指数法在石油开采区土壤PAHs污染分级评价中的应用[J]. 安徽农业科学, 2011, 39(12): 7350-7353.
ZOU Qiao, WANG Yao, DU Xian-yuan, et al. Application of Nemerow index method in grade evaluation of PAHs pollution in the oilfield soils[J]. Journal of Anhui Agricultural Science, 2011, 39(12): 7350-7353. DOI:10.3969/j.issn.0517-6611.2011.12.157
[33]
安婧, 宫晓双, 陈宏伟, 等. 沈抚灌区农田土壤重金属污染时空变化特征及生态健康风险评价[J]. 农业环境科学学报, 2016, 35(1): 37-44.
AN Jing, GONG Xiao-shuang, CHEN Hong-wei, et al. Temporal and spatial characteristics and health risk assessments of heavy metal pollution in soils of Shenfu irrigation area[J]. Journal of Agro-Environment Science, 2016, 35(1): 37-44. DOI:10.11654/jaes.2016.01.005
[34]
刘亚纳, 朱书法, 魏学锋, 等. 河南洛阳市不同功能区土壤重金属污染特征及评价[J]. 环境科学, 2016, 37(6): 2322-2328.
LIU Ya-na, ZHU Shu-fa, WEI Xue-feng, et al. Assessment and pollution characteristics of heavy metals in soil of different functional areas in Luoyang[J]. Environmental Science, 2016, 37(6): 2322-2328.
[35]
杨玉敏, 师学义, 张琛. 基于内梅罗指数法的复垦村庄土壤重金属污染评价及空间分布[J]. 水土保持研究, 2016, 23(4): 338-343.
YANG Yu-min, SHI Xue-yi, ZHANG Chen. Spatial distribution and evaluation of heavy metal pollution of reclaiming village based on Nemerow integrated pollution index method[J]. Research of Soil and Water Conservation, 2016, 23(4): 338-343.
[36]
张金婷, 孙华. 内梅罗指数法和模糊综合评价法在土壤重金属污染评价应用中的差异分析[J]. 环境监测管理与技术, 2016, 28(4): 27-31.
ZHANG Jin-ting, SUN Hua. Differences of Nemerow index method and fuzzy comprehensive evaluation method in evaluation heavy metal pollution in soil[J]. The Administration and Technique of Environmental Monitoring, 2016, 28(4): 27-31.
[37]
李小曼, 徐梦洁, 刘勤, 等. 基于内梅罗指数法及其改进方法的小尺度区域土壤重金属污染评价:以苏南地区为例[J]. 江苏农业科学, 2017, 45(3): 241-245.
LI Xiao-man, XU Meng-jie, LIU Qin, et al. Evaluation of heavy metal pollution of soil in small scale region based on typical and improved Nemerow index method in the case of South of Jiangsu[J]. Journal of Jiangsu Agricultural Science, 2017, 45(3): 241-245.
[38]
林勇. 济南市可耕土壤有机氯、多氯联苯污染分析[D]. 济南: 山东大学, 2011: 40-41.
LIN Yong. Pollution analysis of OCPs and PCBs from soil of Ji'nan[D]. Ji'nan:Shandong University, 2011:40-41. http://d.wanfangdata.com.cn/Thesis/Y1936694
[39]
杨贤智, 李景锟, 廖延梅. 环境管理学[M]. 北京: 高等教育出版社, 1990, 185.
YANG Xian-zhi, LI Jing-kun, LIAO Yan-mei. Environmental management[M]. Beijing: Higher Education Press, 1990, 185.
[40]
Swaine D J. Why trace elements are important?[J]. Fuel Processing Technology, 2000, s65-66(1): 21-33.
[41]
徐争启, 倪师军, 庹先国, 等. 潜在生态危害指数法评价中重金属毒性系数计算[J]. 环境科学与技术, 2008, 31(2): 112-115.
XU Zheng-qi, NI Shi-jun, TUO Xian-guo, et al. Calculation of heavy metals' toxicity coefficient in the evaluation of potential ecological risk index[J]. Environmental Science & Technology, 2008, 31(2): 112-115.
[42]
陈静生, 王忠, 刘玉机. 水体金属污染潜在危害:应用沉积学方法评价[J]. 环境科技(辽宁), 1989, 9(1): 16-25.
CHEN Jing-sheng, WANG Zhong, LIU Yu-ji. Potential risk of heavy metal pollution in water:Assessment by sedimentology measure[J]. Environmental Science and Technology(Liaoning), 1989, 9(1): 16-25.
[43]
林丽钦. 应用毒理学安全评价数据推算重金属毒性系数的探讨[C]//2009重金属污染监测、风险评价及修复技术高级研讨会论文集. 北京: 中华环保联合会能源环境专业委员会, 2009: 57-60.
LIN Li-qin. Discussion on calculation of heavy metals' toxicity coefficient based on toxicological safety evaluation data[C]//Proceedings of advanced seminar on 2009 heavy metal pollution monitoring, risk assessment and remediation technology. Beijing:Energy Resources and Environment Professional Council of All-China Environment Federation, 2009:57-60.
[44]
李雪梅, 王祖伟, 汤显强, 等. 重金属污染因子权重的确定及其在土壤环境质量评价中的应用[J]. 农业环境科学学报, 2007, 26(6): 2281-2286.
LI Xue-mei, WANG Zu-wei, TANG Xian-qiang, et al. Determining weights of heavy metal contaminations and its application to soil environmental quality assessment[J]. Journal of Agro-Environment Science, 2007, 26(6): 2281-2286.