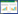文章信息
- 田娜娜, 赵玉杰, 周其文, 刘潇威, 袁旭, 师荣光, 戴礼洪, 徐亚平
- TIAN Na-na, ZHAO Yu-jie, ZHOU Qi-wen, LIU Xiao-wei, YUAN Xu, SHI Rong-guang, DAI Li-hong, XU Ya-ping
- DGT法原位测量水体中金属有效态组分及动力学研究
- In situ measurements of available composition and dissociation kinetics of metals in water using DGT
- 农业环境科学学报, 2017, 36(6): 1210-1217
- Journal of Agro-Environment Science, 2017, 36(6): 1210-1217
- http://dx.doi.org/10.11654/jaes.2017-0150
文章历史
- 收稿日期: 2017-02-09
2. 农业部环境保护科研监测所, 天津 300191;
3. 贵州省农产品质量安全监督检验测试中心, 贵阳 550004
2. Agro-Environmental Protection Institute, Ministry of Agriculture, Tianjin 300191, China;
3. Guizhou Testing Center of Supervision and Inspection for Quality Safety of Agricultural Products, Guiyang 550004, China
水体金属尤其是重金属污染严重威胁水体生态系统健康、影响水生生物安全,并可通过食物链富集最终危害人体。进入水体中的金属会随着水环境如pH、有机质、温度、协同离子浓度等的变化产生形态的转变,造成其环境毒理效应的改变。因此,仅检测金属全量并不能真正指征其环境危害性。近年来,水环境质量安全评价、金属毒性评估、水体污染风险危害预警等研究都涉及到水中金属形态检测、金属配体解离动力学特征分析等问题,如何分析金属不同形态的浓度,计算金属配体解离动力学常数是亟需解决的科学问题[1-2]。
水体金属形态分析主要有下述方法:一种是模型模拟计算法,常用模型为自由离子活态模型、生物配体模型及氧化物表面配体模型等,如WHAM软件采用的Model Ⅶ、SCAMP模型[3],ECOSAT软件采用的道南(NICA-Donnan)模型[4-5],MINTEQ采用的SHM模型[6]等;一种是直接测量的方法,如竞争配体交换耦合差示脉冲阴极溶出伏安法(DPCSV)[7]。模型计算对输入参数要求较高,需了解有机质的组分构成、考虑铁锰氧化物及粘土矿物作用、明确离子之间的交互影响等,因而使用受到限制。直接测量法会受到有机质组分的干扰且存在含量低于检测限而无法检测的问题[8]。
近年来,一种新的技术——梯度扩散薄膜(DGT)技术被应用于水体金属形态分析及运移动力学检测分析。DGT是依据Fick第一定律,通过对特定时间内穿过一定厚度的具有特定功能扩散膜的某一离子进行定量化测量计算而获得某一离子浓度值的原位形态分析技术[9]。DGT技术创新性引入了动态过程概念,且可原位提取活性态金属,避免了易位提取造成的金属形态转化,如Fe、Mn有效态含量的下降[10],因此其获得的金属浓度能更好表征生物有效性,从而被广泛应用于水体、土壤及沉积物金属有效态的测量[11]。
将DGT技术应用于水体金属形态的分析及金属配体解离动力学的研究是DGT研究的新方向,如Zhang等[12]提出可采用不同孔径扩散膜DGT分析金属有效态组分,而Scally等[13]运用不同厚度扩散膜对金属配体解离能力差异性这一特征,提出金属形态分离及配体解离动力学计算的新方法,随后,Warnken等[1]、Cusnir等[14]基于此理论进一步发展了DGT用于水体金属解离动力学的计算方法。然而,以往的技术也存在一定的不足,如Scally方法易存在过拟合现象造成计算结果失真,而Warnken的方法需要借助第三方形态分析软件首先获取水体中金属形态构成,然后计算配体解离动力学特征,这一过程往往引入结果的不确定性。为了更好地将DGT技术应用于水体金属形态分析及配体解离动力学研究,研发一种新的采用DGT技术计算水体金属不同形态含量及金属配体解离动力学方法十分必要。
本研究基于不同厚度扩散膜DGT对金属配体解离能力差异性这一特征,提出了一套计算水体金属配体解离率常数K-1及金属有效态组分的方法,克服了以往计算方法的缺点,具有使用简单、环境条件假设少、获取参数多、结果不确定性小等特点,从而更有利于DGT技术在水体金属污染毒性评估及风险评价中的应用。
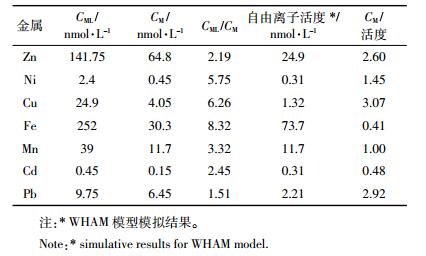
1 理论方法放置于水体中的DGT会通过梯度扩散过程吸附水溶液中的离子态及络合易解离态金属[15],在时间t内DGT累积的金属量计算公式[9]:
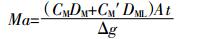 (1)
(1) 式中:Ma为时间t内DGT结合膜上吸附累积的金属量;A为窗口面积,cm2;CM为溶液中金属离子态的浓度;CM′为时间t内由络合易解离金属ML解离的可被DGT测量的金属离子浓度;DM、DML分别为离子及络合态金属在扩散膜中的扩散系数,cm·s-1,通常DML是DM的20%[16];Δg为扩散膜厚度,cm,即为ML解离运移距离,ML在此距离内解离可以被DGT监测到。
联合文献[13]中的公式(6)及公式(7),本文公式(1)中CM′的计算式见式(2):
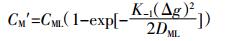 (2)
(2) 式中:K-1为金属ML解离动力学常数。
DGT扩散膜厚度Δg不同,其提供给络合态金属ML的解离时间就有差异性,解离时间的差异造成了不同扩散膜厚度DGT解离浓度CM′的不同。同理,如果把Δg理解为DGT扩散膜厚度差,则CM′就是这一厚度差导致的ML解离量的差值。而如何通过仪器检测计算获得CM′的不同实现是方程(2)获解的关键。
由公式(1)可知,当水体中金属全部为离子态,采用DGT方法获取金属离子的浓度,即有效态金属浓度CM的公式为:
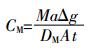 (3)
(3) 当水体中金属全部为离子态,式(3)中CM为一定值,DM、A、t一致时,Ma与Δg呈反比关系。因此,只要通过检测计算出扩散膜厚度为a的DGT的CMa值,则厚度为b(b>a)的DGT其累积的Mab量可通过式(3)计算获得。
当水体中存在金属配体,使金属有效态组分为离子态及络合易解离态时,由于扩散膜厚度增加导致络合易解离态解离量上升,此时扩散膜厚度为b(b>a)的DGT其累积的金属量Mab+会比通过公式(3)理论计算的Mab量高,而增加部分即为DGT增加的厚度Δg(b-a)解离的量,其浓度增量计算公式如下:
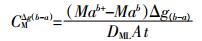 (4)
(4) 
联合公式(2)与公式(4),当水体中存在金属配体时,水体络合易解离态金属ML浓度CML及解离动力学常数K-1的计算公式如下:
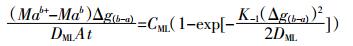 (5)
(5) 采用不同厚度扩散膜DGT测量水体中金属有效态浓度,则式(5)就会有多次实现,从而可以通过非线性拟合方法计算获得CML、K-1等关键参数。进而通过式(1)计算得到CM,则水体中金属有效态浓度为:
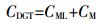 (6)
(6) 确定式(1)中合适的Δg是水体金属有效态浓度计算准确性的关键,Scally等[13]提出当Δg处于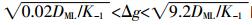
综合分析式(5)可知,当水体中不存在金属配体时,CML及K-1为0,(Mab+-Mab)亦为0,水体金属有效态浓度计算公式可简化为式(3)。当水体中存在金属配体,Δg(b-a)增加且(Mab+-Mab)随之增加,说明DGT实验所选扩散膜厚度使ML始终处于解离增加状态,实验值未达到最大解离,此时采用实验扩散膜最大厚度计算有效态浓度会使计算值小于实际值;当Δg(b-a)增加而(Mab+-Mab)先增加后平稳时,说明DGT实验所选扩散膜厚度使ML达到完全解离,采用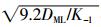
本试验供试水体为天津市津河南开大学段。采样及试验时间为2016年4月12日。DGT原位放置于实验河流水体中,同时用有机玻璃采样器采集试验水样500 mL,用0.45 μm醋酸纤维素滤膜过滤,用于测定水体溶解态金属含量,金属含量检测采用ICP-MS法[17];采集相同水样量用玻璃纤维滤膜过滤,保存在棕色磨口玻璃瓶中用于测定分析DOC(溶解性有机碳),DOC测定采用TOC分析仪。采样水体DOC及金属含量见表 1。
分别制作0.16、0.40、0.8、1.2、2.0 mm厚度的扩散相凝胶。凝胶的准备方法:向10 mL丙烯酰胺凝胶(15%丙烯酰胺,0.3%凝胶交联剂)溶液中加入70 μL 10%的过硫酸铵溶液充分搅拌后加入20 μL四甲基乙二胺(TEMED),搅拌均匀。将溶液快速注入一定厚度的玻璃容器内,并将其平移至恒温恒湿培养箱中,于42 ℃条件下培养1 h,而后取出放在超纯水中,30 min后取出凝胶,24 h内换水至少3次。将制好的扩散相凝胶储存在0.01 mol·L-1的NaCl溶液中备用。
结合相凝胶的准备方法:将用去离子水处理过的200~400目的Chelex-100树脂4 g加入到10 mL丙烯酰胺凝胶溶液中充分搅拌,低温超声2~3 min后加入50 μL 10%的过硫酸铵溶液,并加入15 μL四甲基乙二胺,低温超声1~3 min后将悬浊液快速注入一定厚度的玻璃槽内,将其平移至恒温恒湿培养箱,于42 ℃条件下培养1 h,而后取出放在超纯水中,30 min后取出凝胶,24 h内换水至少三次,将制好的结合相凝胶储存在超纯水中[15]。取制得的扩散相凝胶膜与结合相凝胶膜切割并组装[8],将制好的DGT放于4 ℃冰箱中备用。
2.3 DGT实验将DGT原位放置在河流水体中24 h后取出。将取出的DGT装置用去离子水洗净窗口表面,打开装置将结合相用碳纤维镊子取出放于10 mL塑料刻度试管中,加入2 mL 1 mol·L-1 HNO3溶液,充分脱洗24 h后用去离子水定容混匀,然后吸取1.0 mL的溶液稀释10倍后用ICP-MS(安捷伦7700)测定DGT吸附的金属量。
为了保障实验的精确性及准确性,实验设置4个平行,所有实验用药品全部为优级纯,所用器皿实验前经稀酸处理。实验平行误差控制在10%以内。
2.4 数据处理数据基本计算及拟合计算采用软件DPS 16.05,制图采用微软Excel 2013,水体中金属形态模拟计算采用WHAM 7.04。
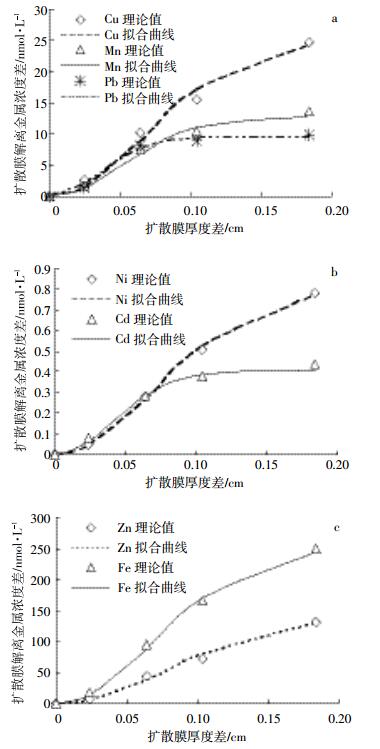
3 结果与讨论 3.1 金属解离动力学参数计算采用式(3)首先计算厚度为0.16 mm(实际计算时需增加硝酸纤维膜保护膜厚度0.13 mm,即0.29 mm)扩散膜DGT的CDGT(0.29)值,然后根据CDGT(0.29)值采用式(3)分别计算扩散膜厚度为0.4、0.8、1.2、2.0 mm的DGT理论计算值Mab,再根据实际检测值Mab+采用式(4)计算获得不同厚度扩散膜DGT解离金属ML浓度差,从而获得式(5)的5次实现。采用DPS软件的非线性拟合中的全局优化算法计算得式(5)中的CML及K-1值,并根据CML及K-1计算最大有效厚度Δg,进而结合式(1)、式(2)及式(6)计算重金属离子态浓度CM及有效态浓度CDGT。方程拟合如图 1所示,计算获得的模型参数K-1拟合结果见表 2,不同金属CM及CML值见表 3。
|
| 图 1不同厚度扩散膜DGT解离金属ML浓度差及拟合结合 Figure 1Fitting models of dissociation concentration difference of metal MLs with different thickness DGT |
结合图 1及表 2可知,模型拟合结果良好,由F显著性检验可知,Zn、Ni、Cu、Fe、Mn、Cd、Pb拟合模型P值均达到极显著水平。
图 1中7种金属的拟合曲线走势表明,随着DGT扩散膜厚度差增加,金属络合物解离浓度也随之增加,在扩散膜厚度差为0.1 cm,实际厚度为0.133 cm以前,处于快速增加阶段,此后增幅下降,Pb、Cd、Mn等增势趋于平稳,其余4种金属依然保持增势。这说明Pb、Cd、Mn的DGT实验厚度已达到了ML全解离的程度,根据解离最大厚度计算公式,可知三种金属络合物ML最大解离厚度分别为0.133、0.126、0.161 cm,本试验最大厚度为0.213 cm,可见试验与理论计算相符。Zn、Ni、Cu、Fe最大解离厚度分别为0.249、0.217、0.208、0.210 cm,略大于或约等于试验最大厚度,说明本试验所选最大厚度基本满足计算金属有效态含量的要求。根据Scally等[13]提出的金属ML有效解离厚度下限计算公式,Zn、Ni、Cu、Fe、Mn、Cd、Pb 7种金属有效解离DGT扩散膜下限值分别为0.012、0.010、0.010、0.010、0.008、0.006、0.007 cm。最小有效解离DGT扩散膜厚度差异进一步表明了金属ML解离难易程度。
不同扩散膜厚度表现出来的金属ML解离浓度值差异性表明,DGT扩散膜厚度对金属有效态的测量有较大的影响,商品化的DGT扩散膜厚度通常为0.093 cm,与Cd、Pb的全解离厚度接近,但远小于其他金属全解离所需厚度。
扩散膜厚度差异性引起的ML解离差异性也表明,水体中金属配体的解离能力是有差别的。通常水体中金属有4种形态:一是离子态,如Cu2+;二是与水中自然存在的配体形成络合物或离子对,如CuCl+、CuCl20;三是与人为引入的配体形成络合物,如与EDTA会形成CuEDTA2-、CuHEDTA-络合体;四是与大分子物质如富里酸,颗粒物(如氧化铁、胶体)等形成络合配体,且FA是由多分子有机酸组成的复合体,存在一价、二价、三价等不同价位配体,不同配体与金属络合稳定性也不同[18-19]。显然金属形态的不同会造成其活性的差异,活性的差异一方面导致其通过DGT扩散膜能力的差别,另一方面与DGT结合相形成络合体的能力也不同。通常高活性的金属形态会更快通过扩散膜并与结合相结合,而低活性的金属形态会较慢地通过扩散膜,并在扩散膜中解离后与结合相结合,当扩散膜厚度达不到使金属络合物解离的厚度时,即使络合物通过了扩散膜也不会与结合相结合,无法被检测到。实验结果表明,在扩散膜厚度低于0.1 cm时,DGT检测到的一般是高活性金属离子及易解离的金属络合物,厚度的增加会导致络合物解离量快速增加;在0.1~0.2 cm厚度时,DGT会增加检测到中等易解离金属络合物的能力,厚度增加会导致解离量及检测值较慢增加;在大于0.2 cm时,不会有更多的络合物被解离,扩散膜厚度增加不会引起检测量增加。
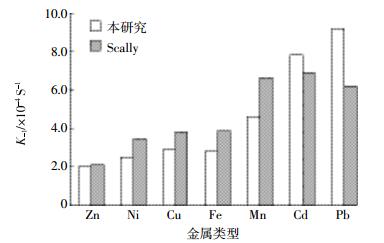
Zn、Ni、Cu、Fe、Mn、Cd、Pb 7种金属络合态ML解离率常数K-1值见表 2,其中Pb的K-1值最大,Cd、Mn次之,Zn最小。根据Scally等[13]提出K-1计算公式(7)计算7种金属的K-1值,其结果见图 2。虽然与本研究的计算值略有差异,但两者趋势基本相同,即Pb、Cd、Mn的K-1值大,而Zn、Ni、Cu小。K-1越大,络合态金属ML越易解离,也进一步说明了Pb、Cd、Mn络合态解离所需DGT扩散膜厚度小的原因。
|
| 图 2采用不同模型计算的不同金属类型K-1值 Figure 2Values of K-1 of different metals with different models |
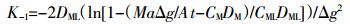 (7)
(7) 采用DGT计算水体中络合态金属ML解离动力学常数K-1,除本研究及Scally等[13]提出的方法外,Warnken等[1]也提出了一套计算模式,其基本计算公式为:
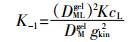 (8)
(8) 式中:DMLgel为络合态金属ML在凝胶扩散膜中的扩散系数;DMLgel为金属M在扩散凝胶中扩散系数;KcL=CML/CM为溶液中金属络合态与离子态浓度的比值,可以通过WHAM、MINTEQ等软件计算获得;gkin为动力限制虚拟距离,可通过式(9)计算获得。
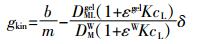 (9)
(9) 式中:b、m分别为不同厚度Δg与DGT检测值1/Ma线性拟合方程的截距与斜率;ε是金属在凝胶及水中扩散系数的比值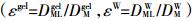
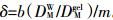
Warnken等[1]提出的方法涉及的计算参数多且需采用第三方软件计算CML及CM,对于较纯净的水体计算相对简单,但对于成分复杂的水体由于污染物含量多,金属之间存在协同或拮抗作用,有机质组分复杂,需要测定有机质中富里酸及腐植酸的构成及组分比例,因此很难精确获得CML及CM值,计算精度难以保证。
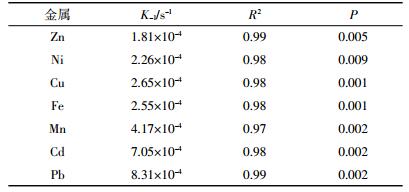
3.2 金属有效态组分分析采用本文提出的方法分别计算金属有效态浓度组分CML及CM,并采用WHAM模型计算水体中自由离子活度值。WHAM计算水体金属离子活度时,假设DOC中50%为活性有机碳,活性有机碳中100%为低分子富里酸[20],结果见表 3。可见除Fe、Cd外,其他5种金属采用本方法计算的离子态浓度CM均大于WHAM模拟计算的自由离子活度。采用DGT技术计算水体金属自由离子浓度与其他静态技术不同,DGT引入了动态化概念,在测定过程中模拟了生物对金属的吸收过程,打破了原系统的平衡,促进了金属配体的解离,从而导致检测获取的CM值增加。可见CM不仅体现了原平衡溶液自由离子活度部分,还应包括其他极易解离的金属配体部分,如水合离子或离子对以及极不稳定的有机络合物等。
采用WHAM模型计算水体中Fe的自由离子活度,我们假设水体中的Fe全部为二价亚铁形式存在,但事实上,自然水体中既存在二价亚铁,也存在三价铁形态[21]。由于同量三价铁的自由离子活度为6.32×10-7 nmol·L-1,几乎可以忽略,WHAM计算所得高的Fe自由离子活度可能与本研究高的亚铁浓度假设有关。
对于Zn、Cu、Pb而言,CM远大于其自由离子活度,进一步计算3种金属水合离子配体(ROH+、R(OH)20)含量值,分别为0.25、0.39、0.42 nmol·L-1,远小于自由离子活度,因此水合配体对CM贡献可以忽略。再采用WHAM模型计算三种金属与富里酸形成非专性吸附与专性吸附浓度比值,分别为57、1、4,远小于Ni、Fe、Cd的该比值(分别为149、209、112),说明在WHAM体系中,Zn、Cu、Pb更易于与有机质形成稳定络合物而使自由离子活度下降,但与本研究的计算结果相比,WHAM有存在过高估计富里酸专性吸附Zn、Cu、Pb的可能。这可能与不同区域水体有机质组成差异性有关,具体原因还需进一步分析。
对于金属Cd而言,其自由离子活度大于CM值,存在WHAM高估自由离子活度的可能性,具体原因还需进一步分析。
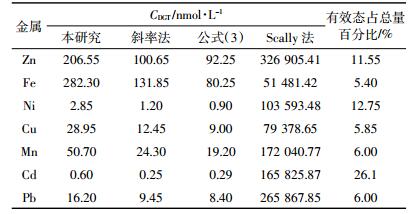
3.3 金属有效态含量计算采用DGT计算水体中金属有效态浓度,主要有4种方法:一是直接采用公式(3)计算[22];二是根据不同厚度扩散膜Δg与DGT检测值Ma倒数所拟合方程计算的斜率m求得,本研究称之为斜率法[23];三是根据Scally等[13]提出的方法通过拟合公式(7)计算获得CM及CML,将两者相加获得,我们称之为Scally法;四是本研究所采用的方法。各方法计算结果见表 4。Scally法虽能计算出CDGT,但由于一个模型有3个参数需估算,且只有5个实现,计算过程易产生过拟合现象。其余三种方法计算结果均表现为本研究提出的方法计算值最大,其次为斜率法,采用公式(3)计算结果最小。可见,采用本方法计算的CDGT能更好地体现有效态中络合易解离部分对全部有效态浓度的贡献,而斜率法其计算初衷是不考虑络合易解离态对CDGT的贡献,采用式(3)计算结果体现的是一定时间内金属M及ML协同供给能力的大小,而计算时仅采用了金属离子的扩散系数DM,偏大的扩散系数及不完全考虑络合易解离态的贡献是其结果偏小的原因。
|
根据金属的解离率常数大小(表 2)、有效态中易解离络合态及金属离子态含量比例大小(表 3)、有效态含量占总量百分比高低(表 4),本研究将金属的性能划分为5类(表 5):一是络合易解离态具有高的解离常数,但相对浓度低,且有效态含量占总量百分比也不高,即有效态中的离子态浓度不高,说明此类金属在水体中形成大分子络合物的能力强,且形成的低分子络合物稳定性差,如Pb、Mn;二是络合易解离态具有低的解离常数,但相对浓度高,且有效态含量占总量百分比不高,说明此类金属在水体中易以有机络合物形式存在,如Fe、Cu;三是金属的解离常数、有效态占总量百分比都高,且有效态中络合易解离态含量低,说明此类金属活性高,形成的络合物稳定性差,如Cd;四是络合易解离态具有低的解离常数,且相对浓度低,但有效态含量占总量百分比高,说明此类金属相对Fe、Cu等金属而言,以离子态形式在水体中存在量大,如Zn;五是络合易解离态具有低的解离常数,但相对浓度高,且有效态含量占总量百分比高,说明此类金属形成的络合易解离态ML虽然解离慢,但浓度高,如Ni。
值得注意的是,本研究所称浓度、含量高低均是相对比较而言,并非真实值的高低,另一方面,金属与有机质形成络合物的形态及解离动力学变化也与水体理化性质有很大的关系,如pH、DOC、富里酸、腐植酸组成等,因此不同水体所获结果可能有一定差异。
4 结论(1)采用本研究提出的计算方法可以不借助第三方金属形态分析软件方便快捷地计算出金属有效态含量、组分构成及K-1值,且计算公式假设参数少,易于拟合,不用考虑其他水环境因子如pH、有机质变化影响。
(2)比较而言,本方法更好地体现出金属有效态中络合易解离部分的贡献,可避免因金属价态、有机质组分构成差异性等因素对有效态含量计算的影响。
(3)根据其形态及运移动力学参数的差异性天津津河7种金属可分为5类:一是Pb、Mn,在水体中形成大分子络合物的能力强,且形成的低分子络合物稳定性差;二是Fe、Cu,在水体中易以有机络合物形式存在;三是Cd,金属活性高,形成的络合物稳定性差;四是Zn,相对Fe、Cu等金属而言,以离子态形式在水体中存在量大;五是Ni,形成的金属络合物解离慢,但相对浓度高。
| [1] | Warnken K W, Davison W, Zhang H, et al. In situ measurements of metal complex exchange kinetics in freshwater[J]. Environmental Science & Technology, 2007, 41(9): 3179–3185. |
| [2] | Wojtkowska M, Bogacki J, Witeska A, et al. Assessment of the hazard posed by metal forms in water and sediments[J]. Science of the Total Environment, 2016, 551: 387–392. |
| [3] | Stockdale A, Tipping E, Lofts S, et al. Dissolved trace metal speciation in estuarine and coastal waters:Comparison of wham/model vii predictions with analytical results[J]. Environmental Toxicology and Chemistry, 2015, 34(1): 53–63. DOI:10.1002/etc.2789 |
| [4] | Fortin C, Couillard Y, Vigneault B, et al. Determination of free Cd, Cu and Zn concentrations in lake waters by in situ diffusion followed by column equilibration ion-exchange[J]. Aquatic Geochemistry, 2010, 16(1): 151–172. DOI:10.1007/s10498-009-9074-3 |
| [5] | Kalis E J J, Weng L P, Dousma F, et al. Measuring free metal ion concentrations in situ in natural waters using the Donnan membrane technique[J]. Environmental Science & Technology, 2006, 40(3): 955–961. |
| [6] | Lourino-Cabana B, Billon G, Lesven L, et al. Monthly variation of trace metals in North Sea sediments:From experimental data to modeling calculations[J]. Marine Pollution Bulletin, 2014, 87(1/2): 237–246. |
| [7] | Xue H B, Jansen S, Prasch A, et al. Nickel speciation and complexation kinetics in freshwater by ligand exchange and DPCSV[J]. Environmental Science & Technology, 2001, 35(3): 539–546. |
| [8] | 赵磊, 崔岩山, 杜心, 等. 利用道南膜技术(DMT)研究土壤中重金属自由离子浓度[J]. 环境科学学报, 2005, 25(11): 1565–1569. ZHAO Lei, CUI Yan-shan, DU Xin, et al. Study on free ion concentrations of heavy metals in soils by Donnan Membrane Technique[J]. Acta Scientiae Circumstantiae, 2005, 25(11): 1565–1569. DOI:10.3321/j.issn:0253-2468.2005.11.022 |
| [9] | Davison W. Diffusive gradients in thin-film for environmental measurements[M]. Cambridge, UK: Cambridge University Press, 2016. |
| [10] | Gimpel J, Zhang H, Davison W, et al. In situ trace metal speciation in lake surface waters using DGT, dialysis, and filtration[J]. Environmental Science & Technology, 2002, 37(1): 138–146. |
| [11] | 罗军, 王晓蓉, 张昊, 等. 梯度扩散薄膜技术(DGT)的理论及其在环境中的应用Ⅰ:工作原理、特性与在土壤中的应用[J]. 农业环境科学学报, 2011, 30(2): 205–213. LUO Jun, WANG Xiao-rong, ZHANG Hao, et al. Theory and application of diffusive gradients in thin films in soils[J]. Journal of Agro-Environment Science, 2011, 30(2): 205–213. |
| [12] | Zhang H, Davison W. Direct in situ measurements of labile inorganic and organically bound metal species in synthetic solutions and natural waters using diffusive gradients in thin films[J]. Analytical Chemistry, 2000, 72(18): 4447–4457. DOI:10.1021/ac0004097 |
| [13] | Scally S, Davison W, Zhang H. In situ measurements of dissociation kinetics and labilities of metal complexes in solution using DGT[J]. Environmental Science & Technology, 2003, 37(7): 1379–1384. |
| [14] | Cusnir R, Jaccard M, Bailat C, et al. Probing the kinetic parameters of plutonium-naturally occurring organic matter interactions in freshwaters using the diffusive gradients in thin films technique[J]. Environmental Science & Technology, 2016, 50(10): 5103–5110. |
| [15] | Zhang H, Davison W, Knight B, et al. In situ measurements of solution concentrations and fluxes of trace metals in soils using DGT[J]. Environmental Science & Technology, 1998, 32(5): 704–710. |
| [16] | Scally S, Davison W, Zhang H. Diffusion coefficients of metals and metal complexes in hydrogels used in diffusive gradients in thin films[J]. Analytica Chimica Acta, 2006, 558(1/2): 222–229. |
| [17] | 环境保护部. HJ 700-2014, 水质65种元素的测定电感耦合等离子体质谱法[S]. 北京: 中国环境科学出版社, 2014. Ministry of Environmental Protection. HJ 700-2014 Water quality-Determination of 65 elements-Inductively coupled plasma-mass spectrometry[S]. Beijing:China Environmental Science Press, 2014. |
| [18] | Hydrology NERC Centre For Ecology. User's Guide to WHAM7[Z]. 2012. |
| [19] | Tipping E. Cation binding by humic substances[M]. Cambridge: Cambridge University Press, 2002. |
| [20] | Sjöstedt C S, Gustafsson J P, Köhler S J. Chemical equilibrium modeling of organic acids, pH, aluminum and iron in Swedish surface waters[J]. Environmental Science & Technology, 2010, 44(22): 8587–8593. |
| [21] | 李和平, 郑泽根. 水体中铁的价态的反相流动注射分析[J]. 土木建筑与环境工程, 1991, 13(1): 89–95. LI He-ping, ZHENG Ze-gen. Analysis of the valence state of iron in water by reversed-phase flow injection[J]. Civil Construction and Environmental Engineering, 1991, 13(1): 89–95. |
| [22] | Zhang H, Davison W. Performance characteristics of diffusion gradients in thin films for the in situ measurement of trace metals in aqueous solution[J]. Analytical Chemistry, 1995, 67(19): 3391–3400. DOI:10.1021/ac00115a005 |
| [23] | Warnken K W, Zhang H, Davison W. Accuracy of the diffusive gradients in thin-films technique:Diffusive boundary layer and effective sampling area considerations[J]. Analytical Chemistry, 2006, 78(11): 3780–3787. DOI:10.1021/ac060139d |
 2017, Vol. 36
2017, Vol. 36