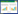文章信息
- 陶双骏, 邵光成, 苏江霖, 李育飞, 张新宇, 张邵华
- TAO Shuang-jun, SHAO Guang-cheng, SU Jiang-lin, LI Yu-fei, ZHANG Xin-yu, ZHANG Shao-hua
- 小流域面源污染风险评估研究——基于多分类有序离散选择模型
- Research on small watershed non-point source pollution risk assessment:Based on the ordered multi-classification discrete choice model
- 农业环境科学学报, 2017, 36(7): 1293-1299
- Journal of Agro-Environment Science, 2017, 36(7): 1293-1299
- http://dx.doi.org/10.11654/jaes.2017-0047
文章历史
- 收稿日期: 2017-01-09
2. 淮安市淮安区水利局, 江苏 淮安 223200;
3. 沭河水利管理局, 山东 临沂 276000;
4. 山东水利职业学院, 山东 日照 276800
2. Water Conservancy Bureau of Huaian District, Huaian City, Huaian 223200, China;
3. Shuhe River Water Management Bureau, Linyi 276000, China;
4. Shandong Water Conservancy Vocational Collage, Rizhao 276800, China
生态清洁小流域是指在传统小流域综合治理基础上,将水土资源保护、面源污染防治、农村垃圾及污水处理等相结合的一种新型综合治理模式[1],最早是由北京市提出的[2],其目标就是保护水源、改善环境、防治灾害、促进发展[3]。近年来随着社会经济的发展,小流域内居民生产生活方式不断发生变化,由流域内的农业生产及居民生活所引起的面源污染已经成为流域水污染的主要因素[4-5]。相对于城市生活及工业生产的点源污染,流域性的面源污染具有污染范围广、随机性大、成分形成复杂等问题,这也加大了流域面源污染的治理难度。
目前对于流域面源污染风险评估研究最常用的方法有事故树分析法、层次分析法、主成分分析法、随机抽样法等,这些方法虽然能为面源污染风险在系统属性评价上提供强大的技术支撑,但是没有考虑到系统中因子的有序性和结构性,而且在利用概率统计方法时将影响因子的贡献值限制在0~1,忽略了单个因子贡献值可能大于1的情况[6-8]。加上对小流域面源污染认识落后,导致现阶段各小流域没有系统的监测资料和详细的基本信息,因而需要探讨一种既符合小流域面源污染监测基础资料匮乏的实际,又能够为小流域面源污染预防与治理提供参考的新方法。本文尝试采用有序多分类离散选择模型对造成小流域面源污染的几个主要因子进行分析,以期建立一种方便、快捷、准确的小流域面源污染风险评估方法。
1 材料与方法 1.1 小流域面源污染风险评估体系构建小流域面源污染主要来源有水土流失、农业面源污染、农村生产生活污染、大气干湿沉降等[9]。由于面源污染具有随机性、多样性、广泛性和不易监测性等特点[10-11],本文在小流域面源污染监测指标体系的基础上,选取泥沙含量、氨氮、总磷、总氮和化学需氧量5个基本环境监测指标,建立小流域面源污染风险评估指标体系,具体如表 1所示。

|
设小流域面源污染风险评估指标集R={x1,x2,…,xn},其中n≥2,xi代表指标集中第i个指标,假定应用因子分析从指标集R中提取出的流域面源污染风险潜在变量为F1、F2、F3。参考环境质量标准对水质污染等级的划分,将污染风险程度设置为“良好、轻度污染、较重污染、重污染、严重污染”,分别用数字“1、2、3、4、5”表示,概率分别表示为P1、P2、P3、P4、P5。影响面源污染的因素有很多,而它们之间存在着多重共线性,因此利用因子分析法提取潜在变量,可有效解决多重共线性问题[15]。因子分析的代数模型如下:
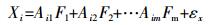 (1)
(1) 式中:X∈R,为观测变量;Fm为风险潜在变量;Aim为潜在变量因子荷载,构成旋转后因子成分矩阵;εx为观测误差或噪声。则有:
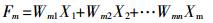 (2)
(2) 式中:Wmn为标准化后的X的加权系数,构成成分得分系数矩阵。
通过因子分析可得出Aim和Wmn分别对应的系数矩阵,从而可用观测变量将潜在变量表示出来。
1.3 建立污染风险评估模型 1.3.1 有序离散选择模型有序多分类离散选择模型不要求变量满足正态分布或等方差性,可对不同程度面源污染的影响因素进行定量评价,在面源污染风险评估中,利用数字来表示风险程度的高低次序,假设y表示在{0,1,2,...,k}上取值的有序分类响应变量,对于其中某一个K值,解释变量为x1,x2,...,xn,则其对应的有序离散选择模型[16-17]为:
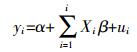 (3)
(3) 式中:yi为第i个研究区域面源污染的风险程度;Xi为第i个区域面源污染风险程度的影响因素向量;α为常数项;β为待估计的系数向量;ui为独立同分布的随机扰动项。
当ui~N(0,1)时,式(3)为有序Probit模型,当ui ~Logistic时,式(3)为有序Logit模型,而Logistic分布模型可以将由解释变量构成的非线性函数转换成线性函数,进而可以判断影响污染的某一种主要因素,并能够计算出不同的自变量,此时各种污染程度的发生概率满足面源污染风险评估的要求。因此,本文采用ui ~Logistic分布的假设。
y表示风险程度,是一个不可观测的值,当实际观测取值时有k种类别,相应取值y=1,y=2,…,y=k,且各取值之间的关系为(y=1) < (y=2) < … < (y=k),这样风险取值就有k-1个未知的临界点,这些点将各相邻的类别划分开[18]。也可表述如下:
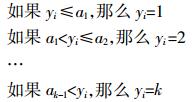 (4)
(4) 式中:ak表示风险的临界点,其值越大代表的风险程度越高;y表示风险程度。
当ui~Logistic分布时,通常使用如下Logistic转换函数:
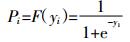 (5)
(5) 可以得到给定X的y的条件分布,即可以计算y取各个值的概率:
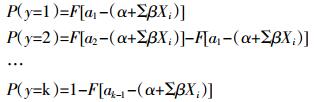 (6)
(6) 式中各项符号表示皆与式(3)、式(4)相同,且:P(y=1)+P(y=2)+…+P(y=k-1)+P(y=k)=1
对于每一个k,都有其对应的似然函数,通过极大似然估计可得到对应临界值a和系数β的极大似然估计值。为简化计算,将似然函数取其对数,求解对数似然函数来估计a和β的值,对数似然函数如下所述[19, 17]:
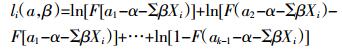
有序Logistic回归模型用于污染风险评估时,通常用“序类数-1”个回归方程描述自变量(预报变量)与响应变量的关系,因此可以用k-1个方程联立给出:
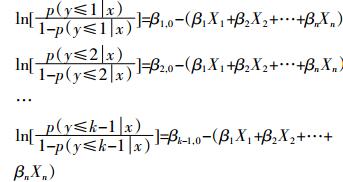 (7)
(7) 式中:等式左边为污染发生比的对数形式,即表示出现某一类状态的机会大小的对数。等式右边X1、X2、…、Xn为预报变量;β1、β2、…、βn为待估计的参数,可通过极大似然估计得到;βn,0表示回归方程截距及未知临界点的集合[17]。
建立的联立方程式(7)经过统计检验后即可对面源污染进行风险分析。将一组污染影响因子数据X1*、X2*、…、Xn*,带入式(7)中,即可求解出p1、p2、…、pn-1的值,进而得到序类1、2、…、n的概率P1、P2、…、Pn:
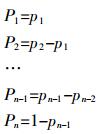 (8)
(8) 式中:Pi =P(y=i),i=1,2,…,k,表示发生某一程度风险的概率。
若
在满足样本多样性的基础上,本文以16个污染程度各不相同的小流域的环境监测数据为基础,对基于有序多分类离散选择模型的小流域面源污染风险评估方法进行了实例分析,其中15个小流域建立模型,第16个为验证模型。分析步骤如下:
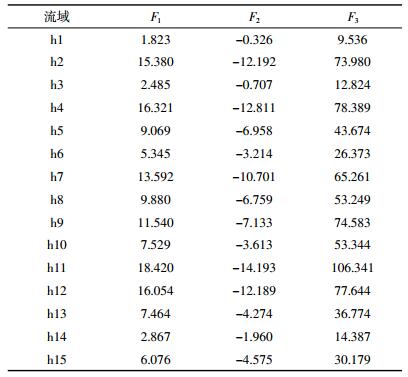
(1)在所选15个小流域数据中,依据小流域面源污染风险评估指标体系(表 1),选择对应流域某一年的监测数据建立小流域风险评估信息表,作为模型分析的样本数据(表 2)。
(2)对表 2的评估信息数据进行Bartlett球体检验、KMO检验,结果显示KMO抽样适度测定值为0.536,大于0.5,Bartlett球形检验值为23.821,P(Sig.=0.008) < 0.05,据此认为该数据可用于因子分析。结果详见表 3。
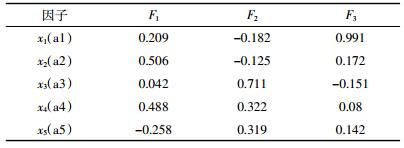
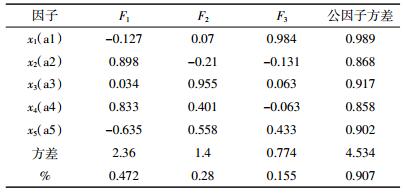
(3)通过因子分析得到成分得分系数(表 4)和旋转成分矩阵和公共因子方差(表 5),以及成分分析碎石图(图 1)和旋转成分图(图 2)。

|
| 图 1成分分析碎石图 Figure 1Scree plot of factor analysis |
|
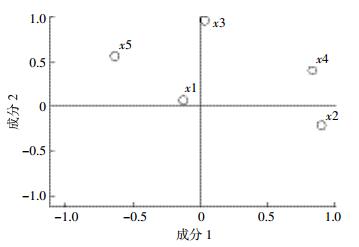
| 图 2旋转空间中的成分图 Figure 2Component plot in rotated space |
根据碎石图(图 1)分析可知,成分1和成分2的特征值均大于1,综合考虑选择因子个数对原变量解释率要高于80%及选取因子的特征值大于1这两个限制条件,选取3个因子,解释率为90.7%。根据旋转成分图(图 2),可认为变量X3、X5是第一组,X2、X4是第二组,X1是第三组。
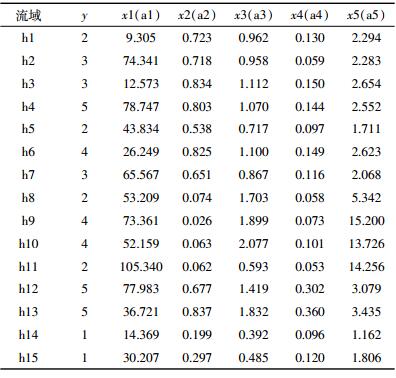
根据表 4,得到如下成分系数方程:
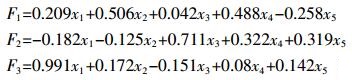 (9)
(9) 式中:F代表潜在变量的成分;x表示污染指标。
由式(9)可知,成分F1,基本支配a2、a4,反映氨氮(NH3-N)和总氮(TN)的情况;成分F2,基本支配a3、a5,反映总磷(TP)和化学需氧量(COD)的情况;成分F3,基本支配a1,反映泥沙含量的情况。
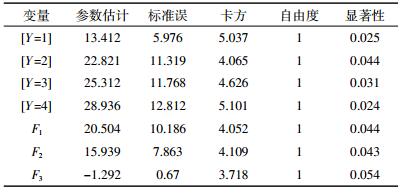
(4)根据提取的潜在变量,通过SPSS 19.0统计分析软件进行有序Logistic回归分析,结果见表 7。
根据以上回归结果建立有序Logistic回归模型:
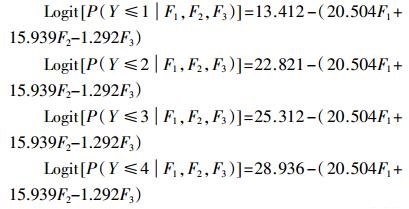 (10)
(10) (5)模型回代估计和预测能力检验
通过Pearson方法和Deviance方法,对模型进行拟合优度检验,结果均表明显著性大于0.9(表 8),可认为拟合结果较好。
将建立模型的样本数据重新带入模型中,通过模型判断的风险程度与流域实际的风险程度的比较,对模型准确性进行验证。准确率η=(1-n/m)100%(其中n表示判错个数,m表示样本总个数),根据表 2数据,利用式(9)、式(10)、式(5)、式(8)计算得到对应风险程度的概率值。结果显示,15个小流域判错3个,准确率为80%。判错的原因可能是样本个数偏少,导致等级3和4的界限区分不够明确,故应增加风险等级3和4的样本数量以明确两者之间的界限。回判分析结果见表 9。
(6)根据小流域面源污染风险评估模型,对第16个小流域进行面源污染风险评估,其面源污染信息如表 10。
根据式(9),提取潜在变量F1=5.418 68,F2= -3.713 11,F3=27.676 6,根据式(10)求解得到待评估区域的p值p1=0.059,p2=0.998,p3=0.999,p4=0.999,根据式(8)得到P值,如表 11。
maxPi =P(y=i)=P2,则可评定区域农业面源污染的风险级别为“2轻度污染”。
(7)通过以上小流域面源污染风险模型的判别分析,认为第16个小流域面源污染风险程度较低,其中污染物中总磷(TP)及化学需氧量(COD)指标较低,泥沙含量、氨氮(NH3-N)、总氮(TN)指标居中。鉴于该小流域主要以农业和旅游业为主,流域内植被丰富、覆盖良好,水土流失量较少,虽然模型预测的污染风险程度较低,但是考虑到引起面源污染的污染物大多吸附在土壤中,尚无随径流进入水体,因此模型预测结果仅供参考。对于该流域,在加强面源污染管理的同时,也要提高流域内居民的环境保护意识,统筹协调流域内的经济发展与生态治理。
3 结论(1)小流域面源污染风险评估指标体系能够满足现阶段小流域面源污染基础资料匮乏的现实,在污染物及污染途径上较好地反映了小流域面源污染的实际情况。
(2)统计样本的回代表明,该模型能够较好地对发生污染的风险进行预测,预测准确率达80%。但由于Logistic模型的判断能力取决于样本数据的准确性及代表性,本模型在样本回代时“较重污染”和“重污染”出现误判,还需进一步增加这两个风险程度在样本中比例。
(3)Logistic模型能够较好地挖掘污染风险等级与影响因子之间的关系,能计算待评估流域面源污染不同风险程度的概率,通过利用观测变量表示潜在变量,从一定程度上解决概率统计方法对影响因子限制的问题。相对于其他判别模型,Logistic模型可为面源污染风险治理提供更多的风险信息,因而是一个相对更优的小流域面源污染风险判别方法。
| [1] | 郝咪娜. 浙江省生态清洁小流域建设措施研究[D]. 西安: 西北农林科技大学, 2013: 1-2. HAO Mi-na. Research on construction measures of eco-clean small watershed in Zhejiang Province[D]. Xi′an:Northwest A&F University, 2013:1-2. http://cdmd.cnki.com.cn/Article/CDMD-10712-1014163174.htm |
| [2] | 毕小刚, 杨进怀, 李永贵, 等. 北京市建设生态清洁型小流域的思路与实践[J]. 中国水土保持, 2005(1): 18–20. BI Xiao-gang, YANG Jin-huai, LI Yong-gui, et al. Reasons and practice on establishing ecological and clean-type small watersheds in Beijing municipality[J]. Soil and Water Conservation in China, 2005(1): 18–20. |
| [3] | 祁生林. 生态清洁小流域建设理论及实践[D]. 北京林业大学, 2006: 23-24. QI Sheng-lin. Study on the eco-clean small watersheds construction theory and practice[D]. Beijing:Beijing Forestry University, 2006:23-24. http://cdmd.cnki.com.cn/Article/CDMD-10022-2006162775.htm |
| [4] | 可欣, 于维坤, 尹炜, 等. 小流域面源污染特征及其控制对策[J]. 环境科学与技术, 2009, 32(7): 201–205. KE Xin, YU Wei-kun, YIN Wei, et al. Some aspects of non-point pollution in small watershed:Characteristics and control strategies[J]. Environmental Science & Technology, 2009, 32(7): 201–205. |
| [5] | 杨艳霞, 曾红娟, 张亚玲. 流域面源污染危害及治理与管理对策分析[J]. 林业调查规划, 2008, 33(6): 43–46. YANG Yan-xia, ZENG Hong-juan, ZHANG Ya-ling. Analysis on harmfulness control and management of non-point source pollution of watershed[J]. Forest Inventory and Planning, 2008, 33(6): 43–46. |
| [6] | 刘建昌, 严岩, 刘峰, 等. 基于多因子指数集成的流域面源污染风险研究[J]. 环境科学, 2008, 29(3): 599–606. LIU Jian-chang, YAN Yan, LIU Feng, et al. Risk assessment and safety evaluation using system normative indexes integration method for non-point source pollution on watershed scale[J]. Environmental Science, 2008, 29(3): 599–606. |
| [7] | Lloyd D K, Lipow M. Reliability:Management, methods, and mathematics[M]. New Jersey: Prentice Hall, Englewood Cliffs, 1962: 291-299. |
| [8] | Saaty T L. How to make a decision:The analytic hierarchy process[J]. European Journal of Operational Research, 1990, 48(1): 9–26. DOI:10.1016/0377-2217(90)90057-I |
| [9] | 余志敏, 袁晓燕, 施卫明. 小流域面源污染治理与评估模型研究进展[J]. 中国人口.资源与环境, 2010, 20(5): 1–4. YU Zhi-min, YUAN Xiao-yan, SHI Wei-ming. Research evolvement of small watershed pollution management and evaluation model[J]. China Population, Resources and Environment, 2010, 20(5): 1–4. |
| [10] | 徐建华. 现代地理学中的教学方法[M]. 北京: 高等教育出版社, 2002: 84-92. XU Jian-hua. Mathematical methods in contemporary geography[M]. Beijing: Higher Education Press, 2002: 84-92. |
| [11] | 张玉斌, 郑粉莉, 武敏. 土壤侵蚀引起的农业非典源污染研究进展[J]. 水科学进展, 2007, 18(1): 123–132. ZHANG Yu-bin, ZHENG Fen-li, WU Min. Research progresses in agricultural non-point source pollution caused by soil erosion[J]. Advances in Water Science, 2007, 18(1): 123–132. |
| [12] | 章茹, 周文斌, 金可礼. 深圳茜坑水库小流域非点源污染负荷估算[J]. 江西师范大学学报(自然科学版), 2008, 32(5): 627–630. ZHANG Ru, ZHOU Wen-bin, JIN Ke-li. Loss of non-point source pollutants from Xikeng Reservoir small watershed in Shenzhen[J]. Journal of Jiangxi Normal University(Natural Science), 2008, 32(5): 627–630. |
| [13] | 卢宝鹏, 张瑞霞. 小流域面源污染监测技术指标体系及监测方法初探[J]. 吉林农业, 2010(9): 157. LU Bao-peng, ZHANG Rui-xia. Preliminary study on monitoring index system and monitoring method of non-point source pollution in small watershed[J]. Jilin Agricultural, 2010(9): 157. |
| [14] | 魏曦, 史明昌, 郭宏忠, 等. 小流域面源污染监测技术体系的构建[J]. 中国水土保持, 2010(11): 14–16. WEI Xi, SHI Ming-chang, GUO Hong-zhong, et al. Construction of monitoring system for non-point source pollution in small watershed[J]. Soil and Water Conservation in China, 2010(11): 14–16. DOI:10.3969/j.issn.1000-0941.2010.11.006 |
| [15] | 牟鹏飞, 张东玲. 有序多分类离散选择模型的信用评级与风险预警研究:以国内20家上市企业为例[J]. 中国海洋大学学报(自然科学版), 2012, 42(9): 90–96. MU Peng-fei, ZHANG Dong-ling. Ordereddiscrete choice model-based credit rating and risk warning:Illustrated by an example of twenty domestic listed companies[J]. Periodical of Ocean University of China, 2012, 42(9): 90–96. |
| [16] | 张冬玲, 高齐圣. 基于多分类离散选择模型的农产品安全风险评估研究[J]. 农业系统科学与综合研究, 2009, 25(1): 5–9. ZHANG Dong-ling, GAO Qi-sheng. Agricultural food safety risk evaluation based on multi-classification discrete choice model[J]. Systemsciences and Comprehensive Studies Inagriculture, 2009, 25(1): 5–9. |
| [17] | 张冬玲. 农产品质量安全综合评价理论与方法研究[D]. 青岛: 青岛大学, 2009: 82-103. ZHANG Dong-ling. Study on theory and method of synthetically evaluation of agricultural products quality and safety[D]. Qingdao:Qingdao University, 2009:82-103. http://cdmd.cnki.com.cn/Article/CDMD-11906-2009128156.htm |
| [18] | 李壁涛. 有序多分类回归模型及其在判断空气质量等级方面的应用[D]. 昆明: 云南大学, 2015: 11-14. LI Bi-tao. The ordinal classification and regression model and its application in judgement the rank of air quality[D]. Kunming:Yunnan University, 2015:11-14. http://cdmd.cnki.com.cn/Article/CDMD-10673-1015609243.htm |
| [19] | 段鹏. 离散选择模型理论与应用研究[D]. 天津: 南开大学, 2010: 27-29. DUAN Peng. Theoreticl research of discrete selection model and its applications[D]. Tianjin:Nankai University, 2015:27-19. http://cdmd.cnki.com.cn/Article/CDMD-10055-1011045764.htm |
 2017, Vol. 36
2017, Vol. 36