文章信息
- 娄永才, 郭青霞
- LOU Yong-cai, GUO Qing-xia
- 岔口小流域非点源污染模型AnnAGNPS不确定性分析
- Uncertainty analysis of an AnnAGNPS model used in the Chakou watershed
- 农业环境科学学报, 2018, 37(5): 956-964
- Journal of Agro-Environment Science, 2018, 37(5): 956-964
- http://dx.doi.org/10.11654/jaes.2017-1272
文章历史
- 收稿日期: 2017-09-19
- 录用日期: 2018-01-10
目前随着点源污染得到有效的治理, 非点源污染成为造成环境污染的首要因素, 是目前治理环境污染的关键。AnnAGNPS模型是众多非点源污染模型中应用最为广泛和成功的模型之一, 是量化和治理非点源污染的重要工具[1-2]。模型所需参数众多, 结构复杂, 参数和输入信息的不准确性会直接导致模型对非点源污染模拟的不确定性。对AnnAGNPS进行不确定性分析是识别模型不确定性来源和度量不确定性的过程。模型的不确定性主要来源于三个方面:模型自身结构的不确定性、模型参数的不确定性、模型输入信息的不确定性[3]。对于模型自身结构的不确定性目前很难对其进行准确量化评价, 一般通过在模型开发中对结构进行改进或模型的选择比较来间接地降低不确定性。因此如何准确量化参数对模型各输出变量不确定性的贡献成为当前迫切需要解决的问题之一。然而目前对参数进行敏感性分析[4-7]的研究较多, 而进一步考虑参数对模型输出变量不确定性的影响相对较少。传统的敏感性分析不能完整描述模型参数的空间分布形态[8], 且存在敏感度低但不确定性高的参数对模型模拟结果的影响可能大于敏感度高但不确定性低的参数的现象[9], 敏感性分析只能给出定性结果, 无法给出定量结果, 因此并不能为准确识别模型的重要不确定性来源提供全面的信息。
本文以典型的黄土丘陵沟壑区——岔口小流域为例, 在参数敏感性分析的基础上, 尝试采用一阶误差分析法(FOEA)和自助法(Bootstrap)对比分析参数的不确定性程度以及对模型输出变量的不确定性的贡献, 以期识别重要的不确定性参数, 提高模型参数的量化能力, 降低模型参数维度以及模拟结果的不确定性, 进而提高模型效率, 以便于模型进一步在流域内推广应用[10]。
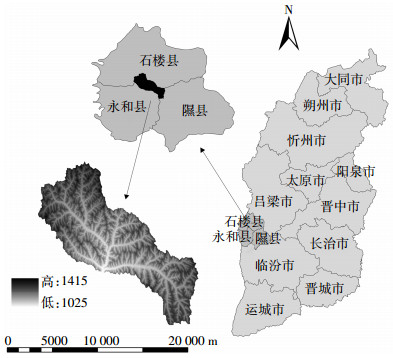
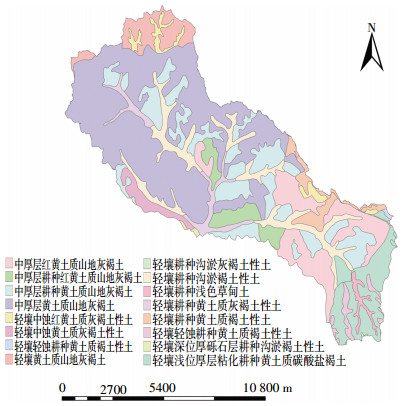
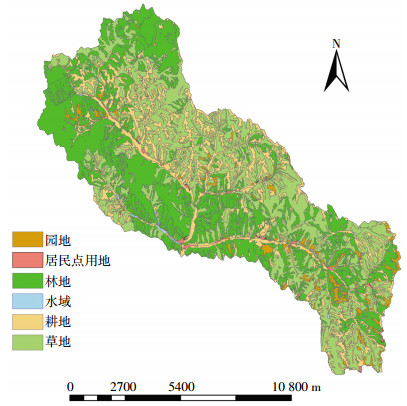
1 材料与方法 1.1 研究区概况岔口小流域位于山西省西南部, 是永和县、石楼县、隰县三者的接壤地带。流域面积131.91 km2, 地处东经110°38'01″~110°50'02″、北纬36°47'26″~36°57'14″, 平均海拔1184 m。研究区属于典型的暖温带半干旱大陆性季风气候, 四季分明, 日照时间长, 多年平均8.6℃, 多年平均降水530.9 mm, 多集中在7-9月三个月, 约占全年降雨量的62.25%。流域内河流属于季节性河流, 丰水期形成历时很短的洪水径流并且径流中携带大量泥沙及营养物质。研究区位于典型的黄土丘陵沟壑区, 流域内沟壑纵横, 支离破碎。流域土壤质地以粉沙质壤土为主, 湿陷性较大。研究区主要包括6种土地利用类型:耕地、园地、林地、草地、水域、居民点, 其中林地、草地所占比重较大。流域内无较大城镇分布、无大型养殖场和工业企业, 因此点源污染可以不用考虑。流域内产业结构单一, 以农业生产为主, 经济发展迟缓。研究区示意图见图 1~图 3。
|
| 图 1 岔口小流域位置 Figure 1 Location of the Chakou watershed |
|
| 图 2 研究区土壤类型 Figure 2 Soil type in the study area |
|
| 图 3 研究区2013年土地利用状况 Figure 3 Status of land use in the study area in 2013 |
AnnAGNPS(Annualized Agricultural Non-point Source Pollution Model)是一种基于日为固定步长对流域一个时间段内每天累计的地表径流、土壤侵蚀、营养盐流失等进行连续模拟的分布式参数模型[16-17]。该模型由美国农业部研发并广泛应用于农业非点源污染研究。其特点包括四个方面:物理概念模型; 输入参数简单; 计算效率高; 能够对流域进行长期模拟监测。
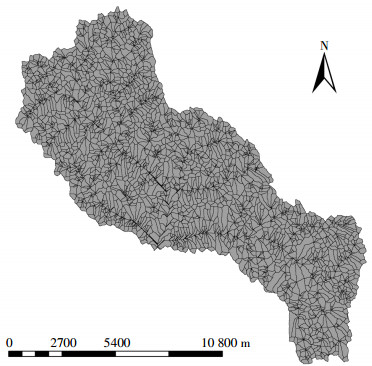
模型包括水文、土壤侵蚀、污染物迁移等模块。基础数据库主要有:气象、地形、土壤、土地利用数据库。研究选用的流域地形数据来源于分辨率为10 m的DEM栅格数据。参考流域第二次全国土地调查土地利用现状数据, 以2013年QuickBird影像为底图进行全流域野外实地调查, 并最终生成2013年1:5万流域土地利用状况图。径流曲线数参考其取值条件和流域不同的土地利用方式、土壤类别、植被覆盖等确定; 流域内作物、田间管理和肥料数据主要通过入户调查和实地采样实测获得; 蓄水坝数据通过岔口小流域坝系工程设计文本和实地调查获得; 土壤数据以1:5万永和县土壤图矢量化得到; 土壤理化性质主要通过实地采样获得。其中, 土壤可蚀性k值是根据土壤粒径含量并参考诺莫图获得; 气象数据为2001-2013年永和县气象站逐日气象资料数据(露点温度、云覆盖、每日地面太阳辐射等通过经验公式间接获得[18-20])和流域内设立的3个雨量监测站实测数据。根据流域实际情况, 最终确定CSA和MSCL值分别为5 hm2和100 m, 将流域划分为8121个子流域(图 4)。在上述基础上将模型所需基础信息数据导入模型输入编辑器, 最终生成Climate.inp和AnnAGNPS.inp, 岔口小流域AnnAGNPS模型初步建成。
|
| 图 4 岔口小流域子流域划分图 Figure 4 The subwatershed of the study watershed based on DEM |
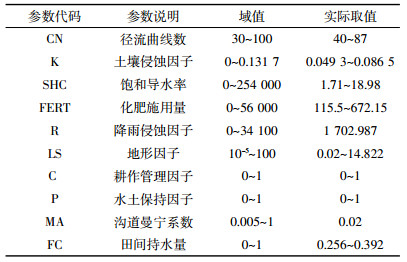
在模型适应性检验[21]的基础上, 基于模型机制结构, 同时兼顾模型操作运算情况, 针对可能对模型输出结果有影响的参数, 筛选出与SCS曲线系数方程、RUSLE方程、营养盐输出模拟过程等有关的10个参数进行敏感性和不确定性分析。各参数取值如表 1所示。
摩尔斯分类筛选法是目前常用的敏感性分析方法之一, 相比于其他方法, 其简单易懂, 且计算量较小, 特别适用于参数较多的复杂模型。经过少量模型计算从而确定参数的定性排序, 识别出相对重要的敏感性参数以达到简化模型的目的。其不足之处在于仅给出定性结果, 无法给出定量结果[10]。在确定模型参数敏感性大小上摩尔斯分类筛选法相对简单有效。本文采用修正的摩尔斯分类筛选法, 在默认各参数之间相互独立的情况下, 选择其中一个参数作为随机变量, 在该变量阈值范围内随机改变变量值, 并将其代入模型从而得到不同的模拟结果, 最终运用基准值来判断各变量对输出值的影响程度[1]。
 (1)
(1) 式中:S为敏感性判别因子; Qi和Qi+1为第i次和第i+1次模型模拟输出值; Q0为参数率定后模型模拟初始值或基准值; Pi和Pi+1为第i次和第i+1次模型运算参数值相对于率定后参数值的变化百分率; n为模型运行次数。
1.3.2 FOEA方法FOEA作为一种不确定分析方法, 目前较多的应用于水文模型的不确定性研究。与传统的敏感性分析不同, FOEA在分析过程中不仅考虑了参数的敏感性, 还考虑了参数的不确定性。该方法可以确定由每个随机输入变量引起的模型输出的不确定性。这种方法来源于泰勒在平均值附近的一系列展开式, 仅取一阶微分[12]:
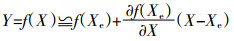 (2)
(2) 式中:Y为模型模拟输出值; f(X)为模型模拟输出值的计算公式; Xe为展开点的矢量。
FOEA中展开点通常设置为平均值或一个中值。因此, 公式的期望值和方差可以近似计算为:
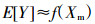 (3)
(3) 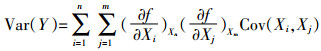 (4)
(4) 式中:Cov(Xi, Xj)为参数XiXj的协方差, 表示两参数之间的相关程度; m、n为参数X的个数。
假设所有参数之间都是相互独立的, 公式(4)可以表示为:
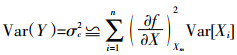 (5)
(5) 参数对总的输出变量的贡献可以表示为:
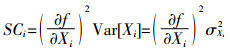 (6)
(6) 式中:SCi为输入参数敏感性的平方乘以参数方差, 该式可以识别和排列特定参数对模型输出的重要性程度。
每个不确定参数对模型总输出方差的贡献可以表示为:
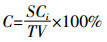 (7)
(7) 式中:C表示贡献率, %; TV表示总方差。
如果参数对总方差的贡献率超过5%[13], 则认为参数是模型不确定性的来源。计算离差系数(CV)值, 该数值表示数据的离散程度或不确定性程度。
1.3.3 Bootstrap方法Bootstrap方法又称自助法, 是Efron于20世纪70年代末提出的。该方法是一种通过重复抽样方法构造自助样本的统计方法, 特别适用于无法采用常规方法对参数进行区间估计、假设检验等[14]。
本文尝试在参数敏感性分析的基础上利用Bootstrap方法对参数进行不确定性分析。以参数标 准差S作为总体标准差σ的估计值; 以参数均值作为总体均值的估计值; 采用变异系数评估参数的不确定性程度; 采用贡献率来评估参数对模型模拟输出结果不确定性的贡献率。具体步骤为:(1)采用Bootstrap方法对参数θ在给定范围内进行随机取样1000次, 得到1000个参数θ*; (2)将1000个参数θ*代入模型得到1000个不同的输出结果Y*(t); 对Bootstrap样本[θ*, Y*(t)]进行验证; (3)求取样本[θ*, Y*(t)]的均值和标准差。
为了定量地表示出参数组合中每个参数对不确定性的贡献程度, 本文引入了一阶误差分析方法中贡献率(Pcv)的概念[15], 计算公式可以表示为:
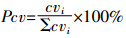 (8)
(8) 式中:cvi表示参数组合中第i个参数的变异系数。
2 分析讨论 2.1 参数敏感性分析采用修正的摩尔斯分类筛选法进行敏感性分析, 计算结果如表 2所示。
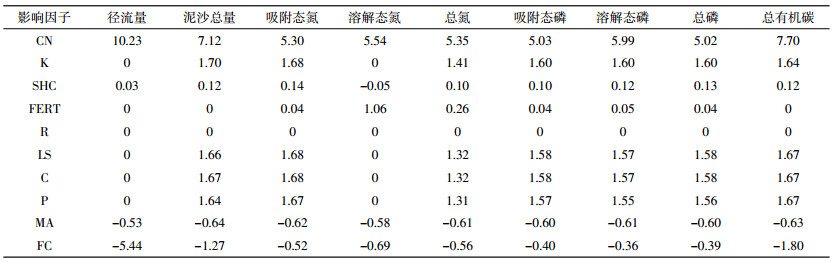
由表 2可以看出, 除降雨侵蚀因子外, 其余参数对模型输出结果均有不同程度的影响。对模型模拟输出结果最为敏感的参数是径流曲线数, 呈明显正相关; 沟道曼宁系数和田间持水量对模型输出结果呈明显负相关。具体来看, 对径流影响最大的是径流曲线数, S值为10.23, 其次是田间持水量, S值为-5.44, 其他参数对径流影响较弱或者无影响。对泥沙量影响最大的是径流曲线数, S值为7.12, 其次是土壤蚀因子, S值为1.70, 此外, 耕作管理因子、水土保持因子和地形因子对泥沙输出量也相当敏感, 这与修正的通用土壤流失方程RUSLE中产沙量主要影响因子相吻合。对总氮、总磷影响最大的是径流曲线数, S值分别为5.35、5.02, 其次是土壤侵蚀因子, S值分别为1.41、1.60, 再次是耕作管理因子, S值分别为1.32、1.58。对总有机碳影响最大的是径流曲线数, S值为7.70, 其次是田间持水量, S值为-1.80, 再次是水土保持因子, S值为1.67。在黄土丘陵沟壑区, 土壤有机碳流失主要以泥沙为承载体被带走, 土壤侵蚀造成了有机碳在泥沙中富集, 且富集比大于1[22], 因此对泥沙敏感程度高的参数对总有机碳的敏感度也高。
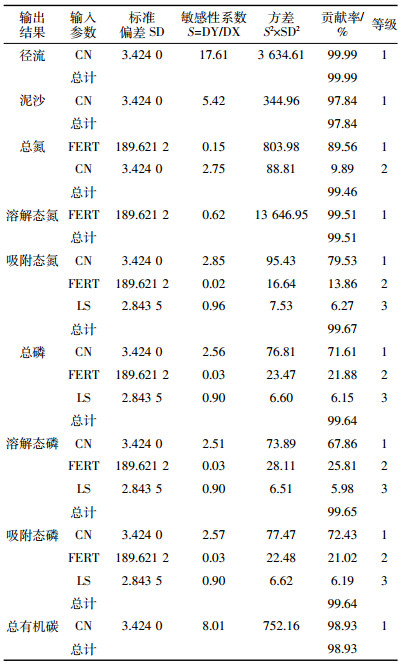
2.2 基于FOEA方法的参数不确定性分析采用FOEA方法对参数进行不确定性分析, 计算结果如表 3所示。
由表 3可知, 径流曲线数对9个输出变量均有显著影响, 其中对径流、总有机碳、泥沙影响最显著, 不确定性贡献率分别为99.99%、98.93%、97.84%。化肥施用量和径流曲线数是总氮较为重要的不确定性参数, 不确定性贡献率为99.46%。对于溶解态氮, 化肥施用量是最为重要的不确定性参数, 不确定性贡献率为99.51%。径流曲线数、化肥施用量、地形因子是吸附态氮、总磷、溶解态磷、吸附态磷较为重要的不确定性参数, 不确定性贡献率为99.67%、99.64%、99.65%、99.64%。
由表 2和表 3可知, 参数敏感性与不确定性排序并不一致, 某些参数敏感性程度高但不确定性却低, 例如总氮的不确定参数中, 化肥施用量的参数敏感性系数为0.26, 但其不确定性贡献率高达89.56%, 而敏感性系数为5.35的径流曲线数的不确定性贡献率只有9.89%。在其他输出结果的不确定参数中同样存在这样的现象。这充分表明敏感性低但不确定性高的参数对模型模拟结果的影响可能大于敏感度高但不确定性低的参数。基于FOEA分析, 可以看出对模型输出结果的不确定性有显著性影响的只有少数几个参数, 而其余参数影响较小或者没有影响。
为了确定参数对不同土地利用类型的影响, 根据公式(6)和公式(7)分别计算了每个参数对不同土地利用类型不确定性的贡献率, 结果如图 5所示。
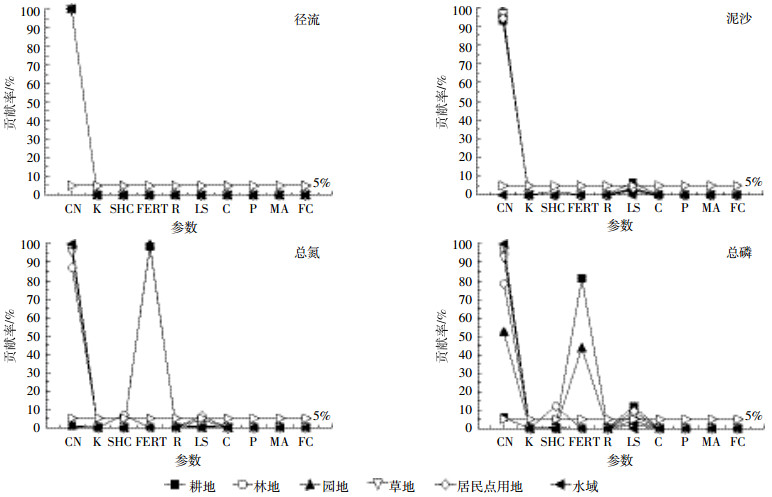
|
| 图 5 参数对不同土地利用类型不确定性贡献率 Figure 5 The contribution of parameters to the uncertainty of different land use types |
由图 5可知, 径流模拟中, 径流曲线数是各类土地利用类型不确定性的主要来源, 其他参数对各地类影响较小或者无影响, 这表明径流曲线数对各地类产汇流起决定性的作用。泥沙模拟中, 除水域外, 径流曲线数对其他土地利用类型影响显著; 地形因子也是耕地不确定性来源, 这主要与耕地中占比较大的坡耕地坡度较大、土质疏松、暴雨季节最易发生土壤侵蚀有关。总氮模拟中, 化肥施用量是耕地和园地不确定性来源, 这主要与耕地和园地施用较多的复合肥有关; 径流曲线数是林地、草地、水域、居民点等不确定性来源, 这四类用地无氮肥施入, 氮流失主要与土壤氮库有关, 且流失形式以溶解态为主; 土壤饱和导水率和地形因子对居民点影响也较大, 流域居民点用地受地形影响坡度起伏变化较大, 植被覆盖度低, 零散禽畜养殖废弃物、居民生活污水、垃圾存在随意排放现象, 在雨季居民点用地地表产流速度较快, 且携带大量污染物。总磷模拟中, 径流曲线数对各地类均有不同程度的影响, 其中对林地、草地不确定性影响最大, 这主要与林草地所占流域面积最大有关; 同总氮模拟一样, 化肥施用量是耕地和园地不确定性来源, 土壤饱和导水率和地形因子也是居民点不确定性来源; 此外, 地形因子也是耕地、草地、居民点等不确定性来源。
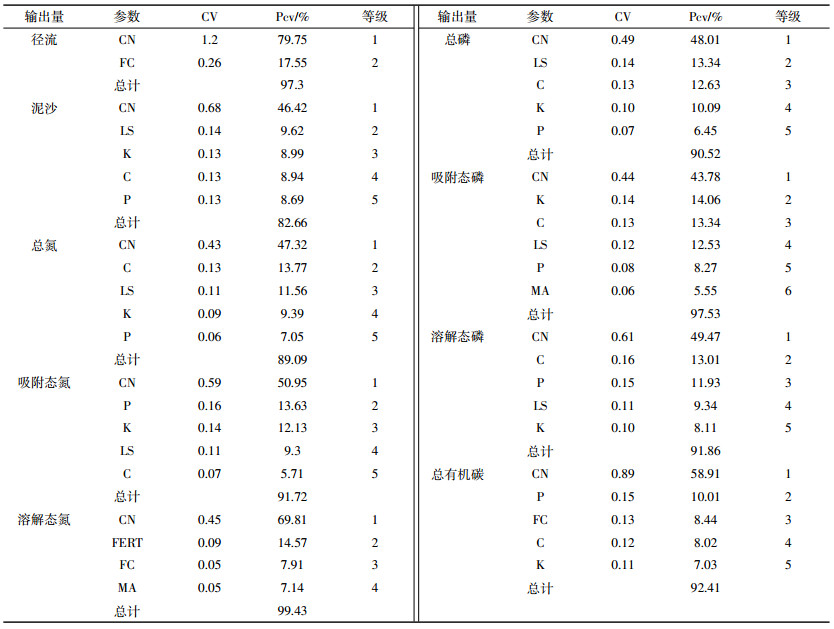
本文采用离差系数来表示模型模拟输出结果不确定性的大小, 离差系数越高, 表明输出结果不确定性越大。计算结果如表 4所示。
由表 4可知, 径流和泥沙离差系数分别为最小和最大, CV值分别为1.12%、11.81%, 表明在模型输出结果中径流具有较小的不确定性, 泥沙具有较大的不确定性。模型模拟输出结果不确定性排序为泥沙>总氮>总磷>径流。
2.3 基于Bootstrap方法的参数不确定性分析在参数敏感性分析的基础上, 利用Bootstrap方法计算参数对模拟结果不确定性的贡献率。计算结果如表 5所示。
由表 5可知, 总体上对模型不确定性具有重要影响的参数主要是:径流曲线数、地形因子、土壤侵蚀因子、耕作管理因子和水土保持因子。
具体来说, 影响模型径流输出不确定性的重要参数是径流曲线数和田间持水量, 这两个参数对径流不确定性贡献率为97.3%。径流曲线数、土壤侵蚀因子、地形因子、耕作管理因子、水土保持因子是影响模型泥沙以及氮磷营养盐输出不确定性的主要参数, 其不确定性贡献总和为82.66%、89.09%、90.52%。化肥施用量、田间持水量、沟道曼宁系数对溶解态氮的影响较大, 其不确定性贡献率总和为29.62%, 这一方面与流域内较多的使用含无机氮比例较高的复合肥有关, 另一方面与流域氮流失主要以溶解态氮为主有关。泥沙和氮磷的不确定性参数较为一致表明:泥沙是氮磷输出的载体, 即在短时暴雨事件下氮磷输出形态通常以泥沙结合态为主, 泥沙的不确定性直接影响和决定氮磷等营养物输出的准确性。通过Bootstrap分析也发现参数的敏感性大小与不确定性大小排序并不一致, 某些参数敏感性程度高但不确定性低。但主要不确定性参数与敏感性较大的参数较为一致。
综上所述, 径流曲线数对模型输出结果的不确定性影响最大。流域内的河流属于季节性河流, 枯水期河道内几乎没有水, 夏季多短时强降雨易造成水土、氮磷等营养物流失, 因此径流是流域泥沙、氮磷流失的外在驱动力。对泥沙负荷模拟计算不确定性影响较大的是径流曲线数、地形因子、土壤侵蚀因子、耕作管理因子、水土保持因子。流域土壤质地以粉沙质壤土为主, 湿陷性较大, 雨季易造成侵蚀。根据闫胜军[23]研究可知流域土壤侵蚀主要集中在坡耕地、坡度较大的低覆盖草地, 且监测期间流域坡改梯工程的实施对土壤扰动强烈, 新修梯田土质疏松、植被覆盖度低、受自然环境影响大, 容易造成水土流失。对总氮、总磷负荷模拟计算不确定性影响较大的是径流曲线数、化肥施用量、耕作管理因子、地形因子、土壤侵蚀因子、水土保持因子。流域氮磷流失主要来源于施肥和土壤氮磷库即由于泥沙的流失引起, 随着施肥量的增加, 氮磷等污染物负荷也相应增加。在雨季农民通过撒施的方式对农作物进行追肥, 这种方式导致农作物对氮磷吸收利用率低, 使得大量氮磷等营养物质通过径流和泥沙进入环境中, 造成环境污染。耕地粗放型的经营方式也增加了氮磷等营养物质流失的风险。
采用FOEA和Bootstrap方法进行不确定性分析, 所得结论与研究区实际情况基本吻合, 这表明采用这两种方法应用于模型不确定性分析具有可行性。基于两种分析方法识别出重要的不确定性参数:一方面能提高模型参数的量化能力, 为模型参数调试提供主要方向, 节省参数调试时间, 从而有利于降低模型不确定性; 另一方面为流域水土流失和非点源污染的治理提供参考和决策依据。
3 结论敏感性分析表明对模型模拟输出结果最为敏感的参数是径流曲线数, 呈明显正相关; 沟道曼宁系数和田间持水量对模型输出结果呈明显负相关。参数的敏感性大小与不确定性大小排序并不一致, 这表明敏感性分析并不能为准确识别模型的重要不确定性参数提供全面的信息。
FOEA和Bootstrap的分析结果表明, 水文参数对模型模拟计算的不确定性贡献最大, 泥沙和氮磷等营养物的不确定性参数较为一致, 因而流域水文和土壤侵蚀过程的模拟成为模型校准、降低不确定性的关键。土壤侵蚀因子和地形因子在一定时间内发生变化的可能性极小, 因此, 结合岔口小流域的实际情况, 在控制和治理流域内水土流失以及非点源污染时应着重考虑径流曲线数、施肥措施、农田管理方式和水土保持情况。
目前基于不同数学理论的不确定性分析方法有很多, 所选的不确定分析方法不同对研究结果产生的影响也不尽相同。为了提高模型预测的精度, 综合分析模型输出的不确定性, 需要更加系统地研究不确定性分析方法, 可以综合运用不同的研究方法, 多途径、多方法地综合分析并合理选用。
| [1] |
王晓利, 姜德娟, 张华. 基于AnnAGNPS模型的胶东半岛大沽河流域非点源污染模拟研究[J]. 农业环境科学学报, 2014, 33(7): 1379-1387. WANG Xiao-li, JIANG De-juan, ZHANG Hua. Simulation of non-point source pollution in Dagu watershed, Jiaodong Peninsula Based on AnnAGNPS model[J]. Journal of Agro-Environment Science, 2014, 33(7): 1379-1387. DOI:10.11654/jaes.2014.07.018 |
| [2] |
涂宏志, 侯鹰, 陈卫平. 基于AnnAGNPS模型的苇子沟流域非点源污染模拟研究[J]. 农业环境科学学报, 2017, 36(7): 1345-1352. TU Hong-zhi, HOU Ying, CHEN Wei-ping. Simulation of non-point source pollution in Weizigou watershed with AnnAGNPS model[J]. Journal of Agro-Environment Science, 2017, 36(7): 1345-1352. DOI:10.11654/jaes.2016-1562 |
| [3] |
廖谦, 沈珍瑶. 农业非点源污染模拟不确定性研究进展[J]. 生态学杂志, 2011, 30(7): 1542-1550. LIAO Qian, SHEN Zhen-yao. Uncertainties in agricultural non-point source pollution simulation:Research progress[J]. Chinese Journal of Ecology, 2011, 30(7): 1542-1550. |
| [4] |
席庆, 李兆富, 罗川. 基于扰动分析方法的AnnAGNPS模型水文水质参数敏感性分析[J]. 环境科学, 2014, 5(35): 1773-1780. XI Qing, LI Zhao-fu, LUO Chuan. Sensitivity analysis of AnnAGNPS model's hydrology and water quality parameters based on the perturbation analysis method[J]. Environmental Science, 2014, 5(35): 1773-1780. |
| [5] |
钟科元, 陈莹, 陈兴伟, 等. 基于农业非点源污染的桃溪流域日径流泥沙模拟[J]. 水土保持通报, 2015, 35(6): 131-134. ZHONG Ke-yuan, CHEN Ying, CHEN Xing-wei, et al. Simulation of daily runoff and sediment load in Taoxi watershed based on AnnAGNPS model[J]. Bulletin of Soil and Water Conservation, 2015, 35(6): 131-134. |
| [6] |
Li A M, Yang H Z, Gui X A. GIS-based decision making analysis of nonpoint source pollution management in Zhangxi River Watershed[C]//3rd International Conference on Bioinformatics and Biomedical Engineering. Beijing: ICBBE, 2009: 1-6. https://ieeexplore.ieee.org/document/5162887/
|
| [7] |
王威, 杨海真, 王少平, 等. 流域非点源分布式模型AnnAGNPS参数的不确定性研究[J]. 四川环境, 2004, 5(27): 44-48. WANG Wei, YANG Hai-zhen, WANG Shao-ping, et al. Study on the uncertainty of the parameters in annualized agricultural non-point source model for river watershed[J]. Sichuan Environment, 2004, 5(27): 44-48. |
| [8] |
余红, 沈珍瑶. 非典源污染不确定性研究进展[J]. 水资源保护, 2008, 24(1): 1-5. YU Hong, SHEN Zhen-yao. Uncertainty of non-point source pollution[J]. Water Resources Protection, 2008, 24(1): 1-5. |
| [9] |
Melching C S, Willy B. Uncertainty in coupled nonpoint source and stream water-quality models[J]. Water Resources Planning and Management, 2001, 127(6): 403-412. DOI:10.1061/(ASCE)0733-9496(2001)127:6(403) |
| [10] |
宋晓猛, 张建云, 占车生, 等. 水文模型参数敏感性分析方法评述[J]. 水利水电科技进展, 2015, 6(35): 105-112. SONG Xiao-meng, ZHANG Jian-yun, ZHAN Che-sheng, et al. Review of methods of parameter sensitivity analysis in hydrologic modeling[J]. Advances in Science and Technology of Water Resources, 2015, 6(35): 105-112. |
| [11] |
郝芳华. 流域非点源污染分布式模拟研究[D]. 北京: 北京师范大学, 2003. HAO Fang-hua. Distributed simulation of non-point source pollution in watershed[D]. Beijing: Beijing Normal University, 2003. |
| [12] |
Shen Z Y, Qian H, Yu H, et al. Parameter uncertainty analysis of non-point source pollution from different land use types[J]. Science of the Total Environment, 2010, 408(8): 1971-1978. DOI:10.1016/j.scitotenv.2009.12.007 |
| [13] |
余红, 沈珍瑶. 三峡水库大宁河流域非点源污染参数的不确定性分析[J]. 中国环境科学, 2007, 27(4): 554-558. YU Hong, SHEN Zhen-yao. Analyzing parameter uncertainty of the non-point source pollution in Daning River of the Three Gorges Reservoir area[J]. China Environmental Science, 2007, 27(4): 554-558. |
| [14] |
马世典, 江浩斌, 吴狄, 等. 基于Bootstrap方法的自动泊车系统精度评价研究[J]. 机械设计, 2014, 12(31): 71-74. MA Shi-dian, JIANG Hao-bin, WU Di, et al. Study on accuracy assessment for auto-parking system based on Bootstrap[J]. Journal of Machine Design, 2014, 12(31): 71-74. |
| [15] |
Shen Z Y, Hong Q, Yu H, et al. Parameter uncertainty analysis of the non-point source pollution in the Daning River watershed of the Three Gorges Reservoir Region, China[J]. Science of the Total Environment, 2008, 405(1/2/3): 195-205. |
| [16] |
Sarangi A, Cox C A, Madramootoo C A. Evaluation of the AnnAGNPS Model for prediction of runoff and sediment yields in St Lucia watersheds[J]. Biosystems Engineering, 2007, 97(2): 241-256. DOI:10.1016/j.biosystemseng.2007.02.015 |
| [17] |
田耀武, 黄志霖, 肖文发. 基于AnnAGNPS模型的三峡库区秭归县非点源污染输出评价[J]. 生态学报, 2011, 31(16): 4568-4578. TIAN Yao-wu, HUANG Zhi-lin, XIAO Wen-fa. Assessment of non-point source pollution export from Zigui County in the Three Gorges Reservoir area using the AnnAGNPS model[J]. Acta Ecologica Sinica, 2011, 31(16): 4568-4578. |
| [18] |
李硕, 刘磊. AnnAGNPS模型在敛水河流域产水、产沙的模拟评价[J]. 环境科学, 2010, 31(1): 50-57. LI Shuo, LIU Lei. Evaluation of AnnAGNPS model for simulation water and sediment yield in the Lianshui River watershed[J]. Environmental Science, 2010, 31(1): 50-57. |
| [19] |
曹文, 申双和. 我国太阳日总辐射计算方法的研究[J]. 南京气象学院学报, 2008, 31(4): 589-591. CAO Wen, SHEN Shuang-he. Estimation of daily solar radiation in China[J]. Journal of Nanjing Institute of Meteorology, 2008, 31(4): 589-591. |
| [20] |
何庆堂. 气象学[M]. 北京: 中国林业出版社, 1986, 52-90. HE Qing-tang. Meteorology[M]. Beijing: China Forestry Press, 1986, 52-90. |
| [21] |
闫胜军, 郭青霞, 闫瑞, 等. AnnAGNPS模型在黄土丘陵沟壑区小流域的适用性评价[J]. 水资源与水工程学报, 2016, 27(1): 13-19. YAN Sheng-jun, GUO Qing-xia, YAN Rui, et al. Suitability evaluation of AnnAGNPS model in Chakou watershed of typical loess hilly region[J]. Journal of Water Resources and Water Engineering, 2016, 27(1): 13-19. |
| [22] |
贾松伟, 贺秀斌, 陈云明, 等. 黄土丘陵区土壤侵蚀对土壤有机碳流失的影响研究[J]. 水土保持研究, 2004, 111(4): 88-90. JIA Song-wei, HE Xiu-bin, CHEN Yun-ming, et al. Effect of soil erosion on soil organic carbon loss on the loess hilly areas[J]. Research of Soil and Water Conservation, 2004, 111(4): 88-90. |
| [23] |
闫胜军. 岔口小流域AnnAGNPS模型验证和坡改梯生态效益分析[D]. 山西: 山西农业大学, 2014. YAN Sheng-jun. Validating the AnnAGNPS model in the Chakou watershed and analyzing the ecological benefit of turning slopeland to terrace[D]. Shanxi: Shanxi Agricultural University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10113-1014416474.htm |
 2018, Vol. 37
2018, Vol. 37