2. 华北理工大学, 河北 唐山 063210
2. North China University of Science & Technology, Tangshan 063210, China
重金属的空间分布及其对生态系统结构功能的影响一直备受关注,其监测与治理已成为国内外科研工作的热点[1-3]。根据2014年发布的“全国土壤污染状况调查报告” [4],我国重金属污染问题严峻,全国污染物的总超标率约为16%,其中铜污染物点位超标率达2.1%。重金属污染具有累积性、隐蔽性、不可逆转性等特点,其在土壤、水体中的富集会对生物有机体产生严重影响。部分重金属离子(如Cu2+)是植物新陈代谢的必要元素,但过量的重金属会对植物细胞产生毒害[1]。并且还会阻碍植物的光合作用,抑制光合产物的输配,影响农作物产量[5-6]。一定浓度的重金属会在植物的根、茎、叶、籽粒部位产生不同程度的累积,进而通过食物链进入人体,危害人类健康。近60年,学者已对植物重金属的吸收和迁移做了大量研究,并提出了土壤-植物系统中元素解吸、迁移、吸收的联合数学模型[7]。重金属污染的监测与治理方面相继发展出物理、化学、生物等方法。传统的植物重金属污染监测方法需使用专业仪器设备、定期观测采样来实现,成本高、过程繁琐、费时费力。而高光谱遥感技术具有较高的光谱分辨率、生化成分反演能力强、便捷、可操作性高和视野宽等优点,为实现大范围实时动态监测提供了可能[8]。因此运用高光谱遥感监测农作物重金属污染是一项具有一定优势的遥感前沿技术。
近年来,有很多学者采用光谱数据的多阶微分、微分光谱角正切、小波变换、经验模态分解(Empirical mode decomposition,EMD)等方法[8-11]对植物叶片原始光谱进行变换以提取反映重金属污染的异常信息,探究不同浓度重金属胁迫下植物的生长状况。就光谱变换与分解方法而言,小波变换缺乏自适应性,必须根据光谱信号的特征选择合适的小波基进行分析,而EMD能以信号本身的局部时间尺度来进行分解,具有良好的自适应性,但分解过程存在模态混叠现象[12]。集成经验模态分解(Ensemble EMD,EEMD)方法克服了模态混叠这一缺点,已经广泛应用于心电信号处理[12]、电力系统故障信号检测[13]、混合信号分离识别[14]等不同领域,同时在土壤剖面反射光谱消噪方面也取得了一定进展[15]。Mallat算法是基于小波分析改进的信号分解和重构方法,已用于数字图像处理[16]、雷达回波去噪[17]、图像增强变换[18]、空气质量指数预测[19]等方面。本文利用EEMD克服模态混叠这一优势,结合MA算法和光谱的分形维数(Fractal dimension,FD)方法,构建不同浓度Cu2+胁迫下玉米叶片污染信息的EEMD-MA-FD光谱诊断模型,用于探测玉米叶片在不同Cu2+污染程度下的光谱弱差信息,为农作物重金属污染监测提供一种新的高光谱遥感应用思路或方法。
1 材料与方法 1.1 胁迫实验与数据采集 1.1.1 植株培养实验选取“密糯8号”玉米作为研究对象,采用有底漏花盆培育玉米种子。对栽培所用颗粒土壤进行碾碎、去除石子及草根杂质、过筛等处理,以逐层喷洒、翻土混合的方式将不同浓度CuSO4·5H2O与土壤充分搅拌均匀并标注相应胁迫浓度。根据《土壤环境质量标准》(GB 15618—1995)中土壤污染标准设置Cu2+胁迫浓度分别为0、200、400、600、800 μg·g-1,记为CK、Cu(200)、Cu(400)、Cu(600)、Cu(800),同一浓度设置3组平行样,共15盆。其中CK组为空白对照组,土壤中本身含有Cu2+,3组平行样Cu2+含量均值为19.6 μg·g-1。2017年5月10日对玉米种子进行催芽处理,5月12日栽培植株,且于生长期定期浇灌并添加适量NH4NO3、KNO3、KH2PO4营养液,培育期间保持各盆栽生长环境一致且通风良好。
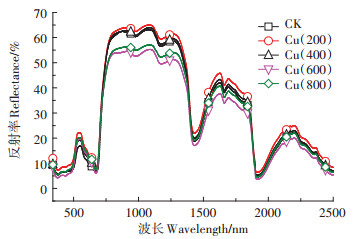
1.1.2 光谱数据获取2017年7月19日,玉米穗期,在暗室内进行光谱数据采集。采用350~2500 nm波谱范围的SVC HR- 1024I高性能地物光谱仪进行测定,测量过程使用50 W的卤素灯作为光源和25°视场角的探头,探头垂直于叶片表面5 cm。为了防止其他物体对玉米叶片光谱的影响,将玉米叶片裁剪后,在遮盖黑布的实验台上进行测定。使用专用白板标准化光谱反射系数。实验选取位于植株上、中、下部位具备代表性的新、中、老叶片的叶中位置进行光谱数据测量,各叶片每次测取3条光谱,取平均值作为最终结果。不同胁迫浓度下玉米叶片均值光谱数据如图 1所示。
|
图 1 不同Cu2+胁迫浓度下玉米叶片光谱曲线 Figure 1 Maize leaf spectra curves stressed by different Cu2+ concentrations |
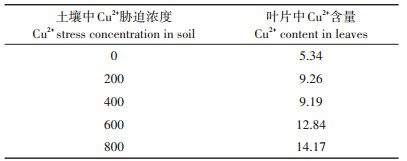
各项实验完成后,采集各胁迫浓度的玉米叶片,进行冲洗、烘干、粉碎等处理,对各个样品封装保存并进行标注、编号。在相同规范条件下,经微波处理后,采用电感耦合等离子发射光谱仪(ICP-OES)对已进行光谱数据采集的老、中、新叶片分别进行Cu元素含量测定,取均值作为每组胁迫浓度叶片Cu2+含量,所测结果如表 1。
|
|
表 1 玉米叶片中Cu2+含量(μg·g-1) Table 1 Cu2+content in maize leaves (μg·g-1) |
EEMD由Wu等[20]提出,主要用于解决EMD存在的虚假分量和模态混叠问题[21]。EEMD的核心是通过多次在原始信号中加入等长度的正态分布白噪声序列,以保证不同尺度信号区域自动映射到与背景白噪声相关的尺度上。将信号和噪声重新组合为一个整体,视为待分解信号,对其进行多次EMD分解,对每次分解的本征模态函数(Intrinsic mode function,IMF)取均值,作为最终结果。需要注意的是,由于每次EMD分解时人为添加的白噪声不同,且噪声之间不具备相关性,因而每次分解所得的IMF分量均会存在微弱差异,当使用足够测试的全体均值时,人为添加的噪声就会被抵消,信号本身是稳固持久的[20]。设一条原始的光谱信号为x(t),则其EEMD处理步骤如下:
Ⅰ为原始光谱信号数据添加一个正态分布的白噪声序列xm(t),即
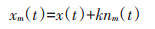
|
(1) |
式中:k为加入背景白噪声的幅值系数;nm(t)为第m次加入的白噪声。
Ⅱ将带有白噪声的光谱信号数据分解成一组IMF分量。
Ⅲ重复执行步骤Ⅰ和步骤Ⅱ,但每次加入不同的白噪声序列。
Ⅳ将每次获得的IMF分量各自取均值作为最终结果。
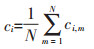
|
(2) |
式中:ci, m为第m次EMD分解得到的第i个分量;N为EMD分解的次数。
1.2.2 Mallat算法(MA)Mallat算法(记为MA)是由Mallat受塔式算法启发于1988年提出的正交小波构造方法,是一种建立在多分辨率基础上进行的分解和重构算法[22]。MA主要是把信号分解为离散平滑分量和离散细节分量,若一光谱信号f(t),Aj为f(t)在第j层低频部分(近似部分)的小波系数,Dj为f(t)在第j层高频部分(细节部分)的小波系数,则MA分解光谱信号的具体算法为[23]:
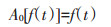
|
(3) |
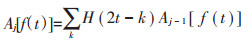
|
(4) |
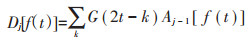
|
(5) |
式中:t为波长;j为层数,j=1,2,…,log2N;k为离散平移位置,k=1,2,…,N;H、G为滤波器系数。可见,Aj是通过第2j-1尺度的小波系数Aj-1与分解滤波器H卷积获得,Dj是通过第2j-1尺度的小波系数Aj-1与分解滤波器G卷积获得[23]。
1.2.3 分形维数(FD)分形理论是一种非线性科学理论,可根据某物质的自相似性描述复杂无序、标度不变的系统,探究混沌事物内部结构[24]。FD是刻画分形体复杂结构的重要工具,反映了复杂形体占有空间的有效性。计算FD的方法有很多,例如量规法、盒维数法、结构函数法等[25-26]。本文采用盒维数法计算光谱曲线的FD,记为D,则[27]:
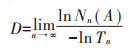
|
(6) |
式中,设A是非空集合,在欧式距离下,用边长为1/Tn的小盒子紧邻地包含A,其中Nn(A)表示包含A所需要的最小盒子数,D为集合A的盒维数。
2 模型应用过程结合EEMD、MA和FD理论与方法,用于不同胁迫浓度下玉米叶片光谱的Cu污染诊断分析,称为玉米叶片Cu2+污染信息的EEMD-MA-FD光谱诊断模型。
2.1 光谱数据的IMF分量提取玉米叶片光谱信号可视为非线性非稳态信号,对不同胁迫浓度的光谱进行EEMD处理,为保证分解有效性,加入的白噪声幅值通常设置在0.01~0.5之间,EMD分解次数设置在100~300之间[20]。本次添加白噪声幅值系数k=0.01,执行EMD总次数为300次。分解后获得各阶IMF(CK时光谱分解的各阶IMF如图 2所示),光谱信号可分解为10阶IMF分量和1阶残余项r。EEMD分解的每一阶IMF分量的振幅与频率均不同,每阶IMF分量在各自特征尺度上具有不同的变化特性。选择可见光及近红外部分波段波长范围在410~780 nm进行探究,对原始光谱反射率与各阶IMF分量之间进行相关性分析,相关系数如表 2所示。根据表 2,比较各IMF分量与原始光谱反射率的相关性,IMF4分量和IMF7分量与原始光谱反射率的相关系数较高,分别为0.755、0.811。并且原始光谱具有在0.54 μm附近形成反射峰,在0.76 μm附近反射率急剧上升的特征,IMF4分量较IMF7分量具有与原始光谱相似的特点,很大程度上保留了原始光谱的特征信息,因此选择IMF4分量对监测重金属Cu2+污染程度具有一定意义。
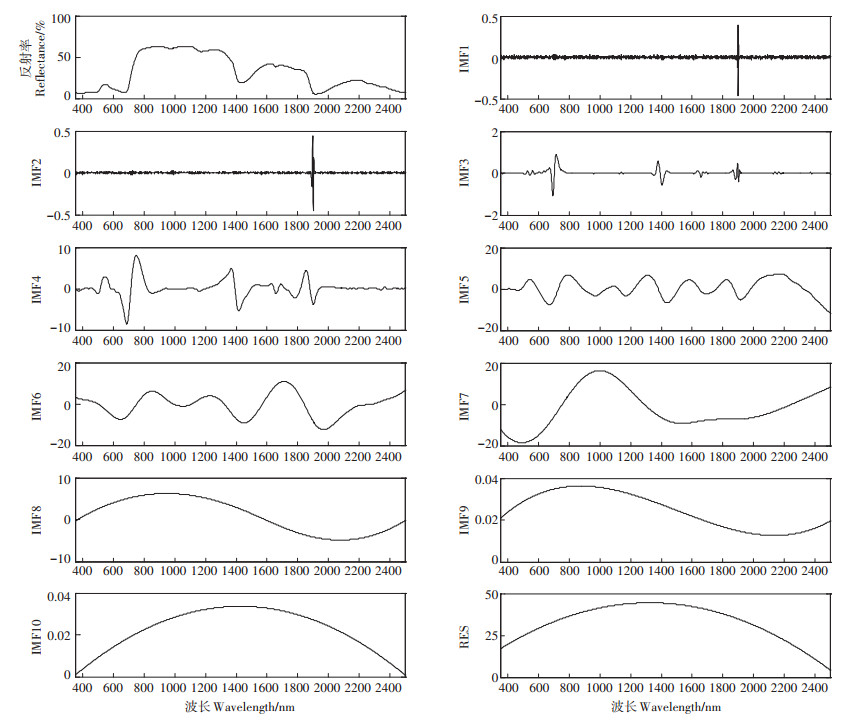
|
图 2 玉米叶片光谱曲线及各IMF分量 Figure 2 Maize leaf spectra curves and various components of IMF |
|
|
表 2 各阶IMF分量与原始光谱相关系数 Table 2 Correlation coefficient between IMF components and original spectra |
对不同Cu2+胁迫浓度的IMF4进行MA变换处理,IMF4分量被分解为逼近信号(sig1)和细节信号(sig2),分解结果如图 3所示。分析图 3发现,不同胁迫梯度sig1与sig2信号在不同波长所对应的振幅与频率均不相同。信号高频部分一般包含突变特征和细节信息等,不同胁迫梯度IMF4分量经过MA低通滤波处理后,分解所得的低频部分(sig1)中细节信息消失,噪声成分被有效去除;经MA高通滤波处理后,IMF4分量中低频部分数据被零替代,高频部分(sig2)保留。

|
图 3 不同胁迫浓度IMF4分量Mallat变换分解结果 Figure 3 The results of Mallat transform decomposition of IMF4 components with different stress gradients |
基于IMF4分量分解的sig1信号和sig2信号计算曲线的分形维数,将结果与相应胁迫浓度玉米叶片Cu2+含量进行相关性分析。sig2分量曲线分形维数与玉米叶片Cu2+含量之间相关性较弱,而sig1信号具有一定的稳定性,其曲线分形维数与对应胁迫浓度玉米叶片Cu2+含量相关性较强,可用指标值刻画其变化情况。将sig1信号分形维数结果记为EEMF,EEMF随玉米叶片Cu2+含量增加而降低,如图 4所示,相关系数为-0.942 2。
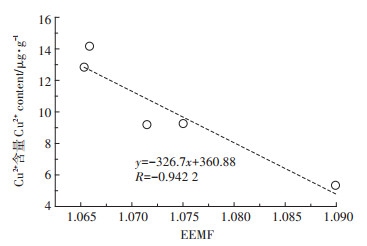
|
图 4 叶片Cu2+含量与EEMF拟合结果 Figure 4 Fitting results on the EEMF and the Cu2+ contents of leaves |
EEMD-MA-FD模型的EEMF随着玉米叶片Cu2+含量增加而降低,为了验证模型的优越性,将模型运用结果分别与传统的监测参数蓝边最大值、红边最大值、红肩最大值进行对比,传统参数的具体定义如表 3所示,分析结果见图 5。蓝边最大值与叶片中的Cu2+含量呈正相关,相关系数为0.907 5,红肩最大值与叶片中Cu2+含量呈负相关,相关系数为-0.801 8,而红边最大值与叶片中Cu2+含量无明显相关性。将经EMD分解、MA变换处理后的分形维数结果记为EMF,分析发现EMF与玉米叶片Cu2+含量无明显相关性,如图 5d所示。由此可证明EEMD-MA-FD模型对监测重金属污染程度具有优越性。
|
|
表 3 玉米叶片的光谱特征参数名称及定义 Table 3 The name and definition of spectral characteristic parameters of maize leaves′ |
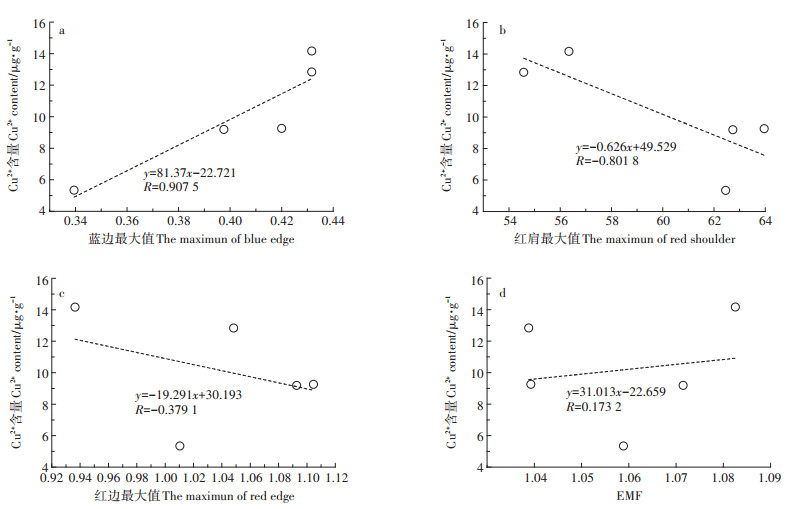
|
图 5 叶片Cu2+含量与各监测方法计算值的拟合结果 Figure 5 Fitting results on the computing values of the monitoring methods and the Cu2+ contents of maize leaves |
为了验证EEMD-MA-FD光谱诊断模型的稳定性,利用2016年培育的“中糯1号”玉米光谱数据进行对比验证。随机选择Cu2+胁迫浓度为0、400、800 μg·g-1的玉米叶片原始光谱数据作为研究对象,计算各胁迫浓度光谱在EEMD-MA-FD模型的EEMF值,并选择红肩最大值与其作对比,结果如图 6所示。EEMF随土壤重金属胁迫浓度的增加呈下降趋势,且与玉米叶片Cu2+含量呈负相关,相关系数为-0.993 7。红肩最大值与叶片中的Cu2+含量无明显相关性。由此可证明EEMD-MA-FD模型稳定性较强,对各品种玉米光谱均可进行良好监测。
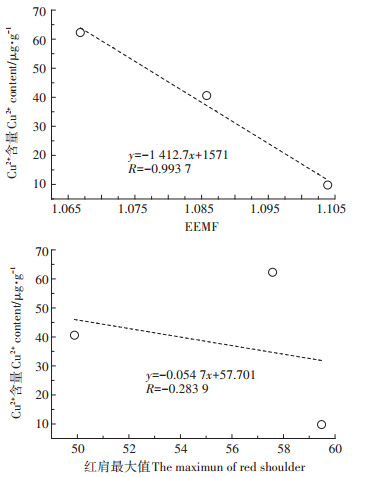
|
图 6 叶片Cu2+含量与EEMF和红肩最大值的拟合结果 Figure 6 Fitting results on the EEMF and the maximun of red shoulder and the Cu2+ contents of maize leaves |
本研究探索性地将EEMD应用于玉米叶片高光谱微弱信息提取中。结果表明,经EEMD分解后IMF4分量与原始光谱相关性较高,并有效抑制噪声。同时结合Mallat算法及盒维数法分形维数构建EEMD-MA-FD光谱诊断模型,并与蓝边最大值、红边最大值等传统监测方法及经EMD分解、MA变换后的分形维数结果分析比较。EEMD-MA-FD模型的EEMF值与玉米叶片Cu2+含量相关性较强,能有效甄别不同Cu2+胁迫浓度的光谱差异,而传统监测方法及EMF值与叶片Cu2+含量均未达到此效果,验证了EEMD-MA-FD模型的优越性。利用另一实验数据对EEMD-MA-FD模型进行的普适性分析,表明EEMDMA-FD模型能够在微弱的光谱差异中识别污染光谱信息,可作为玉米Cu2+污染监测的一种新方法。
| [1] |
王宏镔, 束文圣, 蓝崇钰. 重金属污染生态学研究现状与展望[J]. 生态学报, 2005, 25(3): 596-605. WANG Hong-bin, SHU Wen-sheng, LAN Chong-yu. Ecology for heavy metal pollution:Recent advances and future prospects[J]. Acta Ecologica Sinica, 2005, 25(3): 596-605. DOI:10.3321/j.issn:1000-0933.2005.03.029 |
| [2] |
Clevers J G P W, Kooistra L, Salas E A L. Study of heavy metal contamination in river floodplains using the red-edge position in spectroscopic data[J]. International Journal of Remote Sensing, 2004, 25(19): 3883-3895. DOI:10.1080/01431160310001654473 |
| [3] |
Nayan J K, Parag P, Krishna G B. Assessment of Cd, Co, Cu and B in the shallow aquifers of Jia-Bharali River basin, North Brahmaputra plain, India[J]. International Journal of Environmental Sciences, 2012(4): 1920-1925. |
| [4] |
环境保护部, 国土资源部. 全国土壤污染状况调查公报[J]. 中国环保产业, 2014, 36(5): 10-11. Ministry of Environmental Protection, Ministry of Land and Resources. Bulletin of the national survey of soil pollution status[J]. China Environmental Protection Industry, 2014, 36(5): 10-11. |
| [5] |
赵本行, 陈康姜, 何楚斌, 等. 大豆作物对污染土壤中重金属镉的富集研究[J]. 天津农业科学, 2013, 19(11): 15-17. ZHAO Ben-hang, CHEN Kang-jiang, HE Chu-bin, et al. Cadmium accumulation in soybean crops in contaminated soil[J]. Tianjin Agricultural Sciences, 2013, 19(11): 15-17. DOI:10.3969/j.issn.1006-6500.2013.11.005 |
| [6] |
李裕红, 黄小瑜. 重金属污染对植物光合作用的影响[J]. 海峡科学, 2006(6): 23-24. LI Yu-hong, HUANG Xiao-yu. Effects of heavy metal pollution on photosynthesis of plants[J]. Straits Science, 2006(6): 23-24. DOI:10.3969/j.issn.1673-8683.2006.06.012 |
| [7] |
吴启堂. 一个定量植物吸收土壤重金属的原理模型[J]. 土壤学报, 1994, 31(1): 68-76. WU Qi-tang. A mechanistic mathematical model for predicting the uptake of heavy metals by plants[J]. Acta Pedologica Sinica, 1994, 31(1): 68-76. DOI:10.3321/j.issn:0564-3929.1994.01.009 |
| [8] |
杨可明, 汪国平, 尤笛, 等. 重金属铅离子胁迫下玉米叶片光谱弱差信息的DSAT甄别模型[J]. 光谱学与光谱分析, 2016, 36(8): 2568-2572. YANG Ke-ming, WANG Guo-ping, YOU Di, et al. DSAT model on identifying the weak difference information of corn leaf spectra stressed by heavy metal lead ion[J]. Spectroscopy and Spectral Analysis, 2016, 36(8): 2568-2572. |
| [9] |
王慧, 曾路生, 孙永红, 等. 重金属铜和锌胁迫下的小麦冠层反射光谱特征[J]. 农业工程学报, 2017, 33(2): 171-176. WANG Hui, ZENG Lu-sheng, SUN Yong-hong, et al. Wheat canopy spectral reflectance feature response to heavy metal copper and zinc stress[J]. Transactions of the Chinese Society of Agricultural Engineering, 2017, 33(2): 171-176. |
| [10] |
刘美玲, 刘湘南, 李婷, 等. 水稻锌污染胁迫的光谱奇异性分析[J]. 农业工程学报, 2010, 26(3): 191-197. LIU Mei-ling, LIU Xiang-nan, LI Ting, et al. Analysis of hyperspectral singularity of rice under Zn pollution stress[J]. Transactions of the Chinese Society of Agricultural Engineering, 2010, 26(3): 191-197. |
| [11] |
张婉婉, 杨可明, 汪国平, 等. 基于EMD-SD光谱的玉米叶片叶绿素含量GA-BP模型反演[J]. 浙江农业学报, 2016, 28(8): 1297-1303. ZHANG Wan-wan, YANG Ke-ming, WANG Guo-ping, et al. Study on GA-BP inversing modeling method of corn leaf chlorophyll content based on EMD and spectral derivative method[J]. Acta Agriculturae Zhejiangensis, 2016, 28(8): 1297-1303. DOI:10.3969/j.issn.1004-1524.2016.08.04 |
| [12] |
陈略, 唐歌实, 訾艳阳, 等. 自适应EEMD方法在心电信号处理中的应用[J]. 数据采集与处理, 2011, 26(3): 361-366. CHEN Lue, TANG Ge-shi, ZI Yan-yang, et al. Application of adaptive ensemble empirical mode decomposition method to electrocardiogram signal processing[J]. Journal of Data Acquisition and Processing, 2011, 26(3): 361-366. DOI:10.3969/j.issn.1004-9037.2011.03.020 |
| [13] |
陈可, 李野, 陈澜. EEMD分解在电力系统故障信号检测中的应用[J]. 计算机仿真, 2010, 27(3): 263-266. CHEN Ke, LI Ye, CHEN Lan. Ensemble empirical mode decomposition for power quality detection applications[J]. Computer Simulation, 2010, 27(3): 263-266. DOI:10.3969/j.issn.1006-9348.2010.03.065 |
| [14] |
许舵, 沈国勤, 钱祖平. 基于EEMD方法的混合信号分离识别[J]. 军事通信技术, 2011(2): 29-34. XU Duo, SHEN Guo-qin, QIAN Zu-ping. Research on separation for mixed signals based on ensemble empirical mode decomposition[J]. Journal of Military Communications Technology, 2011(2): 29-34. |
| [15] |
邓凯, 丁建丽, 杨爱霞, 等. EEMD在土壤剖面反射光谱消噪中的应用[J]. 光谱学与光谱分析, 2015, 35(1): 162-166. DENG Kai, DING Jian-li, YANG Ai-xia, et al. EEMD de-noising of reflecting spectrum in soil profiles[J]. Spectroscopy and Spectral Analysis, 2015, 35(1): 162-166. DOI:10.3964/j.issn.1000-0593(2015)01-0162-05 |
| [16] |
刘志轩. 基于二维Mallat算法的数字灰度图像的分解和重构[J]. 农村经济与科技, 2017, 28(8): 337. LIU Zhi-xuan. Decomposition and reconstruction of digital grayscale image based on two-dimensional Mallat algorithm[J]. Rural Economy and Science-Technology, 2017, 28(8): 337. DOI:10.3969/j.issn.1007-7103.2017.08.244 |
| [17] |
李春华, 胡本钧. 基于小波变换Mallat算法的雷达回波去噪[J]. 机电一体化, 2010, 16(2): 51-53. LI Chun-hua, HU Ben-jun. Radar target signal denoising based on wavelet Mallat algorithm[J]. Automation & Instrumentation, 2010, 16(2): 51-53. DOI:10.3969/j.issn.1007-080X.2010.02.010 |
| [18] |
李云, 刘学诚. 一种基于Mallat算法的图像增强方法[J]. 泰山学院学报, 2006, 28(3): 51-53. LI Yun, LIU Xue-cheng. A method of image enhancement based on Mallat algorithm[J]. Journal of Taishan University, 2006, 28(3): 51-53. DOI:10.3969/j.issn.1672-2590.2006.03.014 |
| [19] |
高鹏, 周松林. 基于小波Mallat算法和BP神经网络的空气质量指数预测的研究[J]. 池州学院学报, 2017, 31(3): 42-44. GAO Peng, ZHOU Song-lin. Research on air quality index prediction based on wavelet Mallat algorithm and BP neural network[J]. Journal of Chizhou University, 2017, 31(3): 42-44. |
| [20] |
Wu Z H, Huang N E. Ensemble empirical mode decomposition:A noise assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41. |
| [21] |
孙曙光, 王秋萌, 闫欢, 等. EEMD在电力谐波检测中的应用[J]. 电力系统及其自动化学报, 2016, 28(8): 25-31. SUN Shu-guang, WANG Qiu-meng, YAN Huan, et al. Application of EEMD to power harmonic detection[J]. Proceedings of the CSU-EPSA, 2016, 28(8): 25-31. DOI:10.3969/j.issn.1003-8930.2016.08.005 |
| [22] |
陈艳. 图像处理系统运用POCS-Mallat算法的探讨[J]. 现代工业经济和信息化, 2016, 6(12): 33-34. CHEN Yan. POCS-Mallat algorithm in the application of image processing system research[J]. Modern Industrial Economy and Informationization, 2016, 6(12): 33-34. |
| [23] |
陈进, 王坤, 李耀明. 基于Mallat算法的谷物流量信号小波去噪方法[J]. 农业工程学报, 2017, 33(3): 190-197. CHEN Jin, WANG Kun, LI Yao-ming. Wavelet denoising method for grain flow signal based on Mallat algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering, 2017, 33(3): 190-197. |
| [24] |
张佳瑞, 王金满, 祝宇成, 等. 分形理论在土壤学应用中的研究进展[J]. 土壤通报, 2017, 48(1): 221-228. ZHANG Jia-rui, WANG Jin-man, ZHU Yu-cheng, et al. Application of fractal theory on pedology:A review[J]. Chinese Journal of Soil Science, 2017, 48(1): 221-228. |
| [25] |
李伯奎, 杨凯, 刘远伟. 分形理论及分形参数计算方法[J]. 工具技术, 2004, 38(12): 80-84. LI Bo-kui, YANG Kai, LIU Yuan-wei. Fractal theory and calculation method of fractal parameter[J]. Tool Engineering, 2004, 38(12): 80-84. DOI:10.3969/j.issn.1000-7008.2004.12.030 |
| [26] |
杨可明, 卓伟, 张婉婉, 等. 铜铅重金属胁迫下玉米光谱分形维数与污染监测研究[J]. 科学技术与工程, 2016, 16(24): 228-234. YANG Ke-ming, ZHUO Wei, ZHANG Wan-wan, et al. Study on the fractal dimension and pollution monitoring of corn spectra stressed by heavy metal Cu and Pb[J]. Science Technology & Engineering, 2016, 16(24): 228-234. DOI:10.3969/j.issn.1671-1815.2016.24.042 |
| [27] |
聂笃宪, 曾文曲, 文有为. 分形维数计算方法的研究[J]. 计算机技术与发展, 2004, 14(9): 17-19. NIE Du-xian, ZENG Wen-qu, WEN You-wei. Fractal dimension study of calculating method[J]. Computer Technology and Development, 2004, 14(9): 17-19. DOI:10.3969/j.issn.1673-629X.2004.09.006 |
 2019, Vol. 38
2019, Vol. 38