2. 中国地质大学土地科学技术学院, 北京 100083
2. School of Land Science and Technology, China University of Geosciences, Beijing 100083, China
土壤调查是获取土壤环境状况与污染分布最重要的手段,调查结果的精度直接关系到污染物风险评价的准确性和管理者对于土壤环境决策管理的合理性[1]。其中,点位布设、样品采集、含量分析等各个环节都会导致调查结果的不确定性。土壤本身具有较强的空间异质性,仅提高化验分析与样品采集的精度难以提高土壤污染调查结果的精度。研究表明,针对空间异质性大的要素,点位布设方案是影响调查结果精度的最重要因素之一[1-3]。Gustavsson等[3]在土壤污染调查误差研究中发现,抽样误差是分析误差的20倍以上。Jenkins等[4]在土壤三硝基甲苯污染的研究中表明,至少95%的变异度是由采样位置导致。因此,优化布点方案对提高土壤污染调查结果的精度有着重要作用。
目前,布点方法主要有均匀布点与非均匀布点两种[5]。均匀布点是在缺乏背景信息的情况下,采取诸如随机布点、网格布点等方法布点。而非均匀布点则是在初步调查的基础上,根据已有背景信息,针对性布点。现有的土壤污染调查大多缺乏先验背景信息,以均匀布点居多,多是对研究区内污染物平均水平的估计[6]。而在土壤污染与防治的管理过程中,通常关注于污染位置、范围与程度。因此,以平均水平估计为目的的均匀布点难以满足管理决策需求[7-8]。而在实际的土壤污染调查中,一般分为普查和详查等阶段。普查主要目的是摸清土壤基本情况,识别土壤污染物与大致污染范围,其布点范围广、分布均匀、点位较少。详查则是在普查提供的背景信息的基础上,有针对性地在潜在污染区增加样点,更精确地确定污染类型、污染程度与污染范围,其布点针对性强、区域集中、点位较多。土壤污染布点方案的误差,主要来源于清洁区被高估和污染区被低估[9-10]。前者会增加不必要的修复投入和管理成本,后者则会使污染区不能得到有效的管理与治理。为了降低该类误差,通常会增加样本量,随之而来也增加了成本。高效的布点方案就是要尽可能在降低误差的同时减少成本投入,以最优的资金效率完成土壤污染调查。布点方案优化的目的就是寻找降低调查误差的最优布点区间与样本量。土壤污染同时受气候、地质、水文、生态等背景条件,污染源汇关系以及污染物性质等因素的综合影响,其分布表现出不同的空间相关性和变异性,能否准确判断污染物分布是影响调查结果的关键部分[1]。
近年来,应用地统计学的方法进行土壤污染调查布点与加密布点已成为研究热点[1, 11-17]。该方法基于土壤污染的空间自相关性,运用空间插值或条件模拟的方法,预测土壤污染空间分布,优化点位布局,提高布点效率[9, 11, 15, 18-20]。地统计学中各类方法应用于加密布点的研究已有很多,但大多集中于不同方法在加密布点应用中的可行性研究,而对基于某一方法的不同布点方案的效率(即在固定投入如点位个数情况下,采用不同布点方案带来的调查结果准确性的高低)变化的研究依然十分匮乏。
指示克里金(Indicator kriging)是由Journel(1982)提出的,最初被用于地质统计学处理偏态分布和极值的技术,常用于矿床矿石品位评估。由于土壤污染数据常具有极端值和高偏离度的特性,指示克里金也被广泛应用于土壤污染的研究[21-24]。该方法在普查数据的基础上,通过指示克里金模拟来预测污染物含量超过阈值的概率。指示克里金是一种非参数分布估计方法,该方法基于简单的二元变换,其数据的0~1指示变换使得预测变量对离群值具有的鲁棒性,不存在均匀分布的假设[25]。指示克里金预测值的大小代表大于或小于特定阈值的概率,即从指示数据得出的非抽样地点的期望值等于变量的累计分布[26]。
本研究即聚焦于不同布点方案(加密区域、加密程度)的效率问题和方法优化,以土壤污染详查工作的需求为导向,采用指示克里金的方法确定加密布点区域,对该方法下不同概率区间布点的效率进行比较分析,并对在最优区间内的最优样本量进行了研究,以提高土壤污染布点方案对污染物分布的估计精度,为土壤污染调查提供科学方法的支持。
1 材料与方法 1.1 研究区概况本研究以高原区某山区为例。考虑到样点代表性,选取海拔4200 m以下人类活动较多的区域为案例区。案例区南北跨度25 km,东西跨度40 km,总面积484.01 km2。该地区为灌丛草甸区,以牧草地为主要地类。空气稀薄、干燥,雨季集中在6—9月,年降水量约450 mm,年均气温7.4 ℃,属高原温带半干旱季风气候区。土壤类型主要为高山草甸土,兼有山地灌丛草原土,土体砾石含量高,土层较薄,肥力较低。
研究区内有铅矿开采企业,矿区尾矿中含有大量铅,雨季地表径流冲刷严重,污染物随雨水、河水扩散,导致周边土壤存在较大的铅污染可能性。
1.2 样品采集与测试本案例共采集样点588个,参考500 m×500 m的网格布点,每个样点均采用五点法采样,采样深度20 cm。为防止采样工具对样品造成污染,用不锈钢铲挖好的土方需用木铲对表面剔除,并用木铲取样。
土壤样品铅含量测试:经消解预处理后,采用电感耦合等离子体质谱仪进行检测,根据元素的质谱图或特征离子进行定性,内标法定量。
1.3 方法 1.3.1 基于指示克里金的加密布点区域确定方法在决策管理中,需要治理与否仅取决于污染物含量是否超过某一阈值,基于指示克里金的加密布点方法正是基于该需求提出。
指示克里金[25]首先将污染物浓度值转换为基于某阈值的指示值,如式(1)。假设在研究区A内,设置污染物含量阈值为ZC,则在A内每一个样点X∈A上定义一个ZC的如下阶梯函数:
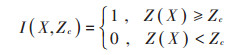
|
(1) |
然后预测单点位置或区域的累积概率,如式(2)和式(3)

|
(2) |
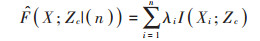
|
(3) |
式中:

将λi带入公式(2)或公式(3)即可得到不超过ZC的累积概率。该方法的误差可以通过式(4)计算[27]。
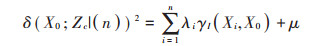
|
(4) |
累积概率的取值范围为0~1。某点位概率越高,其污染的可能性也就越大。污染与否的误判主要来源于污染区与清洁区的过渡区域[7, 28],且为了准确估计污染区范围,该过渡区域应更靠近污染区。过渡区域在概率地图上即表现为某概率区间。只有在该概率区间内加密布点才能提高对污染范围的估计精度。假设过渡区域的概率区间为0.50~0.95,即已经认为概率大于0.95的范围为污染区,概率小于0.50的范围为清洁区。概率在0.50~0.95的范围即为加密布点区,需要进一步调查。
1.3.2 数据处理方法运用指示克里金方法进行概率制图。对污染范围的预测采用序贯高斯模拟方法,该方法是贝叶斯理论的应用,消除了普通插值的平滑效应。运用序贯高斯进行面积预测时,单次模拟存在一定的波动性,需要大量模拟后取均值实现[11]。借鉴已有相关研究经验[11],以及不同模拟次数的实验(500次以上模拟结果基本不会发生变化),为保证研究的准确性,本研究模拟次数为1000次。指示克里金概率制图与序贯高斯模拟预测均在ArcGIS 10.2中实现。
2 案例验证及效率分析以该区域铅污染为例,进行土壤污染调查加密布点区域优化及效率研究。该案例为模拟研究,以500 m×500 m网格辅助参考,一次性采集588个点位,假设以这588个点位近似代表案例区土壤真实情况。运用类似抽样调查的方法,在研究区上叠加1 km×1 km的网格,落在网格内的点作为普查点位,当网格内有多个点位时,随机选取一个作为普查点位,由此获得普查点位共176个。参照《土壤环境质量农用地土壤污染风险管控标准(试行)》(GB 15618—2018),运用序贯高斯模拟分别对总体点位、普查点位、加密后点位进行污染范围预测,以通过总体点位预测的污染面积为基准,分别将通过普查点位和加密后点位预测的污染面积与总体点位预测的污染面积相比较,以此作为普查点位相对总体点位的精度与加密后点位相对总体点位的精度,并将二者进行比较分析,研究不同概率区间内布点效率与最优概率区间内样本量的效率。
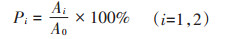
|
(5) |
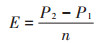
|
(6) |
式(5)为精度计算方法。P1、P2分别表示普查精度和加密布点后精度;A0、A1、A2分别表示总体点位、普查点位、加密布点后点位预测的污染面积。
式(6)为布点效率计算方法。E表示某一概率区间内加密布点的平均效率;n表示该概率区间内加密布点的数量。
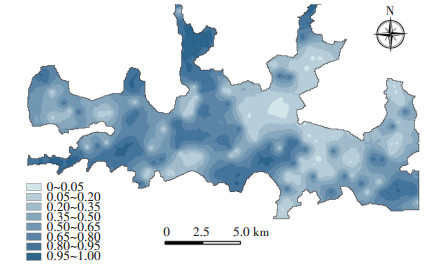
2.1 加密布点区域确定基于普查点位数据,分析其空间分布规律,运用指示克里金方法预测案例区铅污染概率分布,如图 1所示。
|
图 1 基于指示克里金的土壤Pb污染概率 Figure 1 Probability of soil Pb pollution |
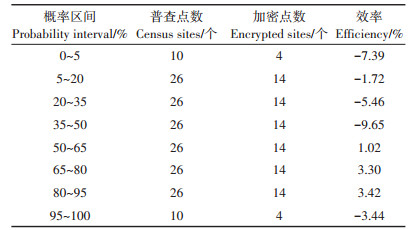
已有研究通过概率制图确定土壤污染调查加密布点区域[1],但目前还没有对不同概率区间加密点位效率的研究。本研究以分析比较不同概率区间加密点位效率为目的,划分了8个概率区间:(0,0.05)、(0.05,0.20)、(0.20,0.35)、(0.35,0.50)、(0.50,0.65)、(0.65,0.80)、(0.80,0.95)、(0.95,1.00)。其中,(0,0.05)与(0.95,1.00)判断为清洁或污染的概率极大,故单独设立区间研究,其余区间均以0.15为步长设立。分别在8个概率区间内均匀随机选择普查点位以外的点模拟加密布点,考虑到数据的有限性以及科学性,在概率介于(0.05,0.95)之间的每个区间设置加密点位14个,在(0,0.05)以及(0.95,1.00)两个概率区间设置4个加密点位,共计92个(图 2a),加密点位与普查点位的分布见图 2b。
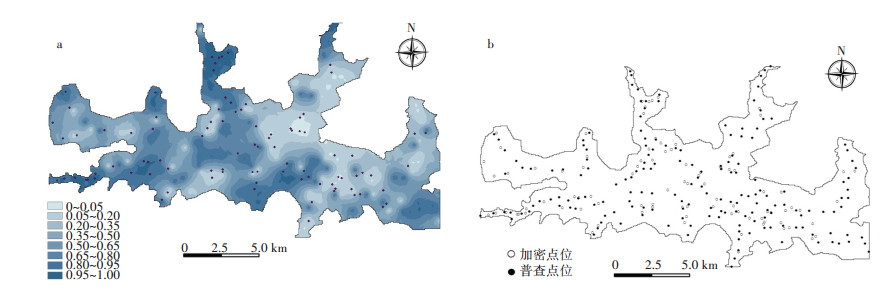
|
图 2 土壤Pb污染调查点位分布 Figure 2 Soil Pb pollution investigation point distribution |
分别对8个概率区间加密后样点进行序贯高斯模拟土壤污染范围,与普查点位模拟的土壤污染范围精度进行比较,以精度的增减来表示效率的高低。结果表明:在非均匀布点的情况下,加密布点不一定能提高土壤污染范围的估计精度,在不合理的区域布点反而会降低土壤污染范围的估计精度。8个概率区间内平均每加密一个点带来的精度变化均不相同,如表 1所示。
|
|
表 1 加密区域效率 Table 1 Efficiency of encryption area |
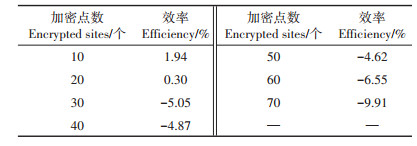
在布点方案的加密工作中,选择合适的样本量既能满足土壤污染范围的估计精度又能减少不必要的投入。在上节研究的基础上,选择概率范围在0.50~ 0.95的区域进行阶梯式加密布点。共设置了7个阶梯,分别加密5.7%(10个)、11.4%(20个)、17.0%(30个)、22.7%(40个)、28.4%(50个)、34.1%(60个)、39.8%(70个)点位。对7个加密后样点分别进行序贯高斯模拟,预测其污染面积。将7个加密样点的精度与176个普查点位精度相比较,以精度的增减来表示效率的高低,结果见表 2。结果表明,在非均匀布点的情况下,加密布点不一定能提高土壤污染范围的估计精度。过密的点位不仅会造成成本的提高,还会降低土壤污染范围的估计精度。在本案例中,加密点数在11.4%(20个)以内会提高土壤污染范围的估计精度,其中以加密5.7%(10个)点位效率最高。当加密点数超过11.4%(20个)时,土壤污染范围的估计精度反而降低,且呈现出随点数增加而效率降低的趋势。
|
|
表 2 加密样本量效率 Table 2 Efficiency of encrypted sample size |
对比588个总体点位,除了0~0.05与0.95~1.00两个概率区间因面积较小加密4个点位外,其余各区间均加密14个点位,即0~0.05与0.95~1.00两个区间加密后点位数为180个,其余区间均为190个。根据结果来看,概率在0.50~0.95之间的区域加密布点时,加密布点对土壤污染范围估计精度有所提升。其中概率在0.65~0.95之间的区域加密布点效率显著高于0.50~0.65区域,点位平均效率达到3%以上,总体精度提高了40%以上。概率在0.05~0.50之间的区域加密布点后效率反而下降,且在这段概率区间内,效率随概率增大而降低。概率在0~0.05以及0.95~1.00之间的极值区加密布点也会造成土壤污染范围估计精度的降低。
这是因为,插值的方法对数据密度的敏感性较高,在数据更密的区域会夸大该类型区域的预测范围。从整个研究区来看,概率0~0.05以及0.95~1.00之间的区域已经有极大概率被判断为清洁区和污染区,在清洁区加密布点会增大清洁区的预测范围,同理,在污染区加密布点会增加污染区的预测范围。即清洁区与污染区内固有的普查点位已足够代表该区域的污染情况,进一步加密布点反而会造成精度的降低与成本的浪费。同样,在靠近污染区的过渡区域(0.50~0.95),其污染可能性较大,但固有的普查点位难以达到对污染范围较高精度的估计,在该区域加密布点会增加污染范围的估计精度。而在靠近清洁区的过渡区域(0.05~0.50),其污染可能性较低,在该区域布点会增加清洁区的估计范围,从而降低污染区范围的估计精度。
从指示克里金的机制来看,概率越接近0.5的区域点位越稀疏,其不确定性越高。本研究为了比较不同概率区间布点效率,对各区间采用均匀布点的方法,因此对于不确定性较高的区域加密布点相对较少。因此也造成了概率区间在0.05~0.50之间区域,效率随概率增加而降低的现象。
以往的调查经验认为,在调查区域布点越密,调查结果越能接近真实情况。造成这个结论的原因是目前大多数土壤调查均属于均匀布点,即在调查区域采用网格布点、随机布点等方法进行布点方案设计。布点越密结果越精确正是在均匀布点的前提假设下才可成立。
在非均匀布点的情况下,在确定的清洁区或污染区加密点位,利用插值方法估计面积,势必会造成对整个研究区预测的清洁面积或污染面积的增加,反而降低了土壤污染范围的估计精度。因此不应在大概率确定污染(清洁)的区域加密布点,而应该在疑似污染但不能确定的区域加密布点。并且,在疑似污染区加密布点的结果精度随加密点数增加呈先增加后降低的趋势。这是由于疑似污染区随着加密点位的增多,判断为污染区或清洁区的概率逐渐增大,最终变成确定的污染区或清洁区,若继续加密布点就会夸大该区域的面积,从而降低精度。这与往常采用均匀布点方法的情况有所不同。
简单来说,假设研究区为A,加密区为B,即有B ⊆A,若B为大概率判断为清洁区或污染区(已知区域),用加密布点的数据来估计A的情况势必会造成误判(若只用加密布点的数据仅对B进行估计是可以有效提升精度的);若B为不确定区域(未知区域),用加密布点的数据对A的情况进行估计是有可能提高估计精度的(是否可以提高还需看加密的点数是否合适)。
4 结论与局限 4.1 研究结论本研究优化了基于指示克里金的确定土壤污染调查加密布点区域的方法,即利用已有调查数据,采用类似抽样调查的方法先进行模拟加密布点,确定加密布点最优布点区域以及加密程度,在此基础上再进行正式加密。该方法的意义不仅在于节省了调查成本,更在于提高了结果精度,避免了无目的加密造成的预测偏差。
在该方法的基础上研究了不同概率区间内的加密布点效率与加密样本量的效率。结果表明:在非均匀布点的前提下,加密布点不一定能提高土壤污染范围的估计精度。在确定的清洁区或污染区加密布点以及在疑似污染区加密布点过密,都会降低整个研究区土壤污染范围的估计精度,在疑似污染区加密适当的点位数才有助于估计精度的提高。案例研究显示:
(1)概率在0.50~0.95之间的区域,加密布点对土壤污染范围估计精度带来了提升;概率在0.05~0.50之间的区域加密布点效率反而下降;概率在0~0.05以及0.95~1.00之间的极值区加密布点也会造成土壤污染范围估计精度的降低。
(2)加密点数在11.4%(20个)以内会提高土壤污染范围的估计精度,而当加密点数超过11.4%(20个)时,土壤污染范围的估计精度反而降低,且呈现出随点数增加而效率降低的趋势。
4.2 局限性(1)由于土壤污染空间分布较为复杂,不同尺度下土壤污染分布规律可能会有所不同,由本案例得出的结论是否适用于更大尺度的区域,还需要做进一步的研究。
(2)本案例区属于高原区土壤铅污染较重区域,由本案例得出的结论是否适用于不同地形区域、不同污染物、不同污染程度区域,还有待进一步的研究。
(3)本研究所提出的优化基于指示克里金的确定土壤污染调查加密布点区域的方法仅适用于达到一定点位数量的大中型规模调查,小规模调查点位较少不足以支撑模拟研究。
| [1] |
谢云峰, 曹云者, 杜晓明, 等. 土壤污染调查加密布点优化方法构建及验证[J]. 环境科学学报, 2016, 36(3): 981-989. XIE Yun-feng, CAO Yun-zhe, DU Xiao-ming, et al. Development and validation of a sampling design optimization procedure for detailed soil pollution investigation[J]. Acta Scientiae Circumstantiae, 2016, 36(3): 981-989. |
| [2] |
Theocharopoulos S P, Wagner G, Sprengart J, et al. European soil sampling delines for soil pollution studies[J]. The Science of the Total Environment, 2001, 264(1/2): 51-62. |
| [3] |
Gustavsson B, Luthbom K, Lagerkvist A. Comparison of analytical error and sampling error for contaminated soil[J]. Journal of Hazardous Materials, 2006, 138(2): 252-260. DOI:10.1016/j.jhazmat.2006.01.082 |
| [4] |
Jenkins T F, Grant C L, Brar G S, et al. Sampling error associated with collection and analysis of soil samples at TNT-contaminated sites[J]. Field Analytical Chemistry & Technology, 2010, 1(3): 151-163. |
| [5] |
姜成晟, 王劲峰, 曹志冬. 地理空间抽样理论研究综述[J]. 地理学报, 2009, 64(3): 368-380. JIANG Cheng -sheng, WANG Jin-feng, CAO Zhi-dong. A review of geo-spatial sampling theory[J]. Acta Geographica Sinica, 2009, 64(3): 368-380. DOI:10.3321/j.issn:0375-5444.2009.03.012 |
| [6] |
Brus D J, Spätjens L E E M, Gruijter J J D. A sampling scheme for estimating the mean extractable phosphorus concentration of fields for environmental regulation[J]. Geoderma, 1999, 89(1/2): 129-148. |
| [7] |
刘庚, 毕如田, 张朝, 等. 某焦化场地苯并(a)芘污染空间分布范围预测的不确定性分析[J]. 环境科学学报, 2013, 33(2): 587-593. LIU Geng, BI Ru-tian, ZHANG Chao, et al. Uncertainty analysis on spatial distribution prediction of BaP in a cokoing plant site[J]. Acta Scientiae Circumstantiae, 2013, 33(2): 587-593. |
| [8] |
谢云峰, 陈同斌, 雷梅, 等. 空间插值模型对土壤Cd污染评价结果的影响[J]. 环境科学学报, 2010, 30(4): 847-854. XIE Yun-feng, CHEN Tong-bin, LEI Mei, et al. Impact of spatial interpolation methods on the estimation of regional soil Cd[J]. Acta Scientiae Circumstantiae, 2010, 30(4): 847-854. |
| [9] |
赵倩倩, 赵庚星, 姜怀龙, 等. 县域土壤养分空间变异特征及合理采样数研究[J]. 自然资源学报, 2012, 27(8): 1382-1391. ZHAO Qian-qian, ZHAO Geng-xing, JIANG Huai-long, et al. Study on spatial variability of soil nutrients and reasonable sampling number at county scale[J]. Journal of Natural Resources, 2012, 27(8): 1382-1391. |
| [10] |
Marchant B P, Mcbratney A B, Lark R M, et al. Optimized multiphase sampling for soil remediation surveys[J]. Spatial Statistics, 2013, 4(1): 1-13. |
| [11] |
谢云峰, 杜平, 曹云者, 等. 基于地统计条件模拟的土壤重金属污染范围预测方法研究[J]. 环境污染与防治, 2015, 37(1): 1-6. XIE Yun-feng, DU Ping, CAO Yun-zhe, et al. Estimating the area of heavy metal contaminated soil using geostatistical conditional simulation[J]. Environmental Pollution Control, 2015, 37(1): 1-6. |
| [12] |
D'Or D. Towards a real-time multi-phase sampling strategy optimization[M]. Springer Berlin Heidelberg: Geostatistics for Environmental Applications, 2005: 355-366.
|
| [13] |
Demougeot-Renard H, De F C, Renard P. Forecasting the number of soil samples required to reduce remediation cost uncertainty[J]. Journal of Environmental Quality, 2004, 33(5): 1694-1702. DOI:10.2134/jeq2004.1694 |
| [14] |
Juang K W, Lee D Y, Teng Y L. Adaptive sampling based on the cumulative distribution function of order statistics to delineate heavymetal contaminated soils using Kriging[J]. Environmental Pollution, 2005, 138(2): 268-277. |
| [15] |
Groenigen J W V, Siderius W, Stein A. Constrained optimisation of soil sampling for minimisation of the Kriging variance[J]. Geoderma, 1999, 71(3): 239-259. |
| [16] |
Tooren C F V, Mosselman M. A Framework for optimization of soil sampling strategy and soil remediation scenario decisions using moving window Kriging[M]. Springer Netherlands: geoENVI-Geostatistics for Environmental Applications, 1997: 259-270.
|
| [17] |
Verstraete S, Van M M. A multi-stage sampling strategy for the delineation of soil pollution in a contaminated brownfield[J]. Environmental Pollution, 2008, 154(2): 184-191. DOI:10.1016/j.envpol.2007.10.014 |
| [18] |
Webster R, Burgess T M. Optimal interpolation and isarithmic mapping of soil properties Ⅲ changing drift and universal kriging[J]. European Journal of Soil Science, 2010, 31(3): 505-524. |
| [19] |
Englund E J, Heravi N. Conditional simulation:Practical application for sampling design optimization[M]. 1993: 613-624.
|
| [20] |
阎波杰, 潘瑜春, 赵春江. 区域土壤重金属空间变异及合理采样数确定[J]. 农业工程学报, 2008, 24(增刊2): 260-264. YAN Bo-jie, PAN Yu-chun, ZHAO Chun-jiang. Spatial variability and reasonable sampling number of regional soil heavy metal[J]. Transactions of the CSAE, 2008, 24(Suppl 2): 260-264. |
| [21] |
杨奇勇, 杨劲松, 余世鹏. 禹城市耕地土壤盐分与有机质的指示克里格分析[J]. 生态学报, 2011, 31(8): 2196-2202. YANG Qi-yong, YANG Jin-song, YU Shi-peng. Evaluation on spatial distribution of soil salinity and soil organic matter by indicator Kriging in Yucheng City[J]. Acta Ecologica Sinica, 2011, 31(8): 2196-2202. |
| [22] |
Meirvenne M V, Goovaerts P. Evaluating the probability of exceeding a site-specific soil cadmium contamination threshold[J]. Geoderma, 2001, 102(1): 75-100. |
| [23] |
Castrignanò A, Goovaerts P, Lulli L, et al. A geostatistical approach to estimate probability of occurrence of Tuber melanosporum in relation to some soil properties[J]. Geoderma, 2000, 98(3/4): 95-113. |
| [24] |
Lin Y P, Chang T K, Shih C W, et al. Factorial and indicator Kriging methods using a geographic information system to delineate spatial variation and pollution sources of soil heavy metals[J]. Environmental Geology, 2002, 42(8): 900-909. DOI:10.1007/s00254-002-0600-5 |
| [25] |
Cressie N. Statistics for spatial data[J]. Technometrics, 1992, 35(3): 321-323. |
| [26] |
Smith J L, Halvorson J J, Papendick R I. Using multiple-variable indicator Kriging for evaluating soil quality[J]. Soil Science Society of America Journal, 1993, 57(3): 743-749. DOI:10.2136/sssaj1993.03615995005700030020x |
| [27] |
Gao B, Liu Y, Pan Y, et al. Error index for additional sampling to map soil contaminant grades[J]. Ecological Indicators, 2017, 77: 129-138. DOI:10.1016/j.ecolind.2017.02.011 |
| [28] |
Xie Y, Chen T B, Lei M, et al. Spatial distribution of soil heavy metal pollution estimated by different interpolation methods:Accuracy and uncertainty analysis[J]. Chemosphere, 2011, 82(3): 468-476. DOI:10.1016/j.chemosphere.2010.09.053 |
 2019, Vol. 38
2019, Vol. 38