2. 农业部农业信息技术重点实验室, 北京 100097;
3. 北京农业信息技术研究中心, 北京 100097;
4. 国家农业信息化工程技术研究中心, 北京 100097;
5. 中国科学院地理科学与资源研究所资源与环境信息系统国家重点实验室, 北京 100101
2. Key Laboratory of Agri-informatics, Ministry of Agriculture, Beijing 100097, China;
3. Beijing Research Center for Information Technology in Agriculture, Beijing 100097, China;
4. National Engineering Research Center for Information Technology in Agriculture, Beijing 100097, China;
5. State Key Laboratory of Resources and Environmental Information System, Institute of Geographic Sciences and Natural Resources Research, CAS, Beijing 100101, China
随着城镇化和工业化的不断发展,土壤重金属污染问题日趋显著,对人类健康和农产品安全构成严重威胁,亟需寻求有效的应对措施[1-2]。根据土壤环境质量将农田划分为不同的等级,是进行差别化管理和治理的前提条件。《土壤污染防治行动计划》强调,要实施农用地分类管理,保障农业生产环境安全[3]。土壤环境质量等级划分一般通过将污染物含量与相关标准和研究规定的阈值对比来实现,如原环保局制定的《土壤环境质量标准》(GB 15618—1995)[4]和原环保部制定的《食用农产品产地环境质量评价标准》(HJ/T 332—2006)等[5]。目前,采样依然是土壤重金属含量调查最主要的技术手段[6-10],基于稀疏样本数据获得目标区域农田的重金属等级,需要基于样本数据进行空间上的插值。
空间插值方法可以分为确定性方法和统计学方法两类。确定性方法如反距离插值、样条函数等,确定性方法只能给出未知点的估计值,但是不能给出估计值的不确定性。由于样本数据不足及土壤重金属含量机理不清,插值结果存在一定误差,需要结合插值结果的不确定性对插值结果进行解读。统计学方法能够同时给出未知点的估计值和估计值的不确定性,适用于土壤重金属含量插值。简单克里金、普通克里金或趋势克里金等方法常用于土壤重金属含量插值[11],并通过将插值结果与等级划分阈值进行对比,进而划分农田土壤重金属含量等级。由于其插值结果存在一定的平滑效应,使得较小值和较大值向中间值靠拢,当阈值较大或者较小时,根据插值结果和阈值关系进行等级划分容易产生错误[12-13];另外,这几种克里金插值需要基于估计误差服从正态分布的前提假设,而实际土壤重金属样点数据一般具有较高的偏度,并不满足该假设。土壤重金属含量等级划分具有不同于含量插值的特点,它只需准确估计未知点上的含量与等级划分阈值之间的大小关系,而并不需要精确含量值。指示克里金是一种非参数地统计方法,它通过直接与阈值进行对比将含量数据转化为0和1的指示值,能够直接推断得到未知点重金属含量小于阈值的概率,能够减少含量值平滑后的等级划分误差,也不需要限定重金属含量的分布类型,更适合用于农田土壤重金属等级划分[14-16]。
由于政府管理部门和研究机构对农田环境的长期重视,在实际工作中,很多区域积累了多期农田土壤重金属采样数据。而目前采用多期土壤重金属样点数据的研究主要集中于对多期土壤样品重金属含量的统计特征对比和分析[17-19],或是采用相关时空地统计模型对重金属含量分布进行预测[20];针对土壤重金属进行等级划分的研究则主要基于某一期土壤重金属含量数据计算地累积指数、潜在风险系数、内梅罗污染指数等来进行风险等级划分[21-23],利用多期数据对土壤重金属的等级划分目前研究较少。由于在时间维度上,不同时期的土壤重金属含量数据间具有一定差异性,如果直接将时间尺度上所有时期数据整合成某一时期的数据直接进行插值,时间变异性将转变成空间上的变异性,引入了时间变异的误差,这将影响最终的等级划分结果,因此需要充分利用多期时空采样数据来提高农田土壤重金属质量等级划分的精度。在本研究中,采用基于时空指示克里金插值的方法从时空角度对土壤重金属质量等级划分展开研究,并分析土壤重金属的等级分布特征及等级划分的不确定性,以期为科学管理和决策提供一定数据基础,促进土地资源有效利用,为政府的土壤环境等级划分工作提供辅助支撑。
1 材料与方法 1.1 研究区北京市,位于华北平原北部,总面积16 410.54 km2,其中山地约占总面积的62%,平原约占总面积的38%。平均温度为8~12 ℃,年平均降水量584 mm左右。其区域图如图 1所示,地形西北高、东南低,母质类型多样。北部丘陵地区成土母质以片麻岩、花岗岩、安山岩为主,西部以灰岩和砂页岩为主;平原地区成土母质质地疏松,以砂壤、轻壤和黄土性母质为主。受地形和母质类型的影响,远郊区以生产小麦、玉米和水稻为主,而近郊区以蔬菜、果树和农田防护林为主。随着北京城郊农业和现代化农业发展,大量农药、化肥和有机肥投入逐年增加。污灌面积也在急剧增加,目前北京地区污水灌溉面积近800 km2,占全市耕地面积的19%,占灌溉农田面积的24%,其中大多分布在通州、大兴、朝阳、房山等北京城水流下游郊区县。
|
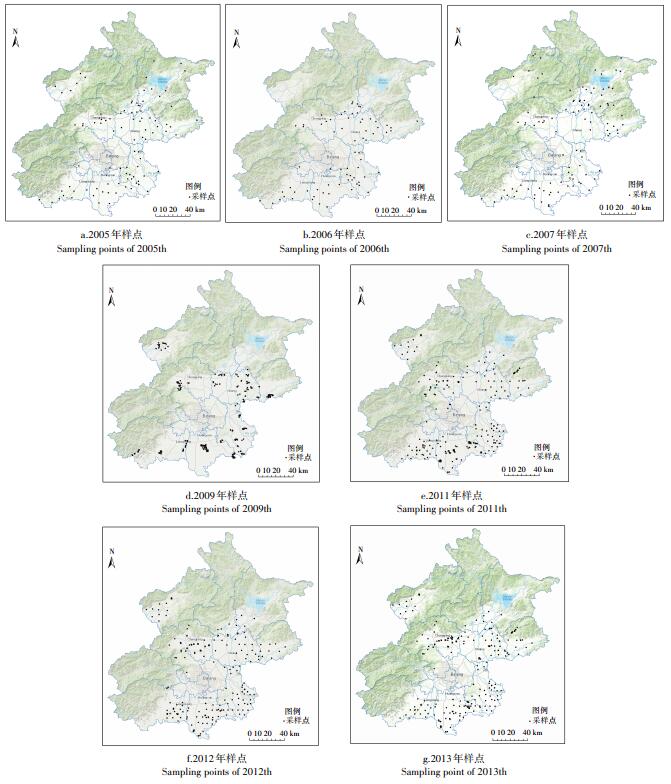
图 1 研究区样点 Figure 1 The sampling points of study area |
基于由北京市农林科学院相关团队管理的农产品质量与农田环境基础数据平台,本研究从中分别提取了2005、2006、2007、2009、2011、2012、2013年这7年的农田土壤重金属采样点数据,这些样本均是基于相同的方法进行采集和测定。采集时使用GPS定位,基本覆盖北京市农田区,其点位分布情况如图 1所示。每个样点单元均为边长10 m的正方形,并在每个单元内的土壤表层0~25 cm深度范围内采集3~5个点。按四分法取1.0 kg分析样品作为代表该点的混合样品,土壤样品经王水水浴加热消解,重金属镉的含量由石墨炉原子吸收法测定,在分析过程中引入重复样品和质控样品进行质量监控。
1.3 时空指示克里金时空指示克里金方法首先将原变量值转换成为指示变量[24],如公式(1)所示[25]:
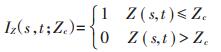
|
(1) |
式中:IZ(s,t;Zc)为基于阈值Zc的指示值;Zc为阈值;Z (s, t)为原变量值;s为某空间研究区域;t为某时间。
某时间t内具有全覆盖数据的研究区域s,不超过阈值Zc的累积概率可以通过指示值进行计算:
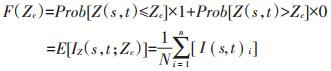
|
(2) |
式中:F(Zc)为不超过阈值的累计概率;Prob[Z(s,t)]≤ Zc)为小于阈值的概率(或者频率);E[IZ(s,t;Zc)]为基于某时间段某空间范围内指示值的期望值。研究区域基于阈值的累积概率可以转化为指示值的期望值。
针对在未抽样点处,随机变量Z(s,t)低于阈值的累积概率同样可以使用样本点指示值的加权获得,同时指示变量的无偏最优估计结果即为Z(s,t)累积概率的无偏最优估计结果。即:
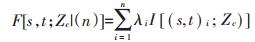
|
(3) |
式中:F[s,t;Zc |(n)]为随机变量低于阈值的累计概率;λi为相应样本点指示值的权重。
类似于普通克里金,以公式(3)中估计结果的无偏最优作为限制条件,求解加权系数,计算未抽样点上目标变量低于阈值的累积概率估计值及其估计误差。
为了求解无偏最优估计,基于平稳假设,需要定义基于样本指示值计算的半变异函数,基于样本指示值计算的时空半变异函数[26]:

|
(4) |
式中: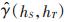
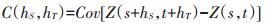
|
(5) |
针对时空半变异函数相关学者们进行了大量研究[27-31]。如度量模型、乘积模型等。这些模型也被相关学者用于气温、水、辐射监测、疾病等领域进行时空插值研究[32-37]。本研究是将时间差异性和空间差异性结合在一起进行研究,因此采用的是时空和度量模型(SumMetric Model)[38],该模型能拟合出时空地理数据的时空变异结构,其时空半变异函数可以表示为:

|
(6) |
式中:γ(hS,hT)为时空半变异函数;γ(hS)为空间尺度半变异函数;γ(hT)为时间尺度半变异函数;γST(hsT)为时间与空间相互关系的半变异函数。
1.4 基于时空指示克里金的等级划分在进行等级划分中,根据一定的阈值将研究区域的研究对象划分成相应的等级。基于时空指示克里金的等级确定的基本步骤如下:
(1)指示变换:确定k个等级阈值Zc1,Zc2,…,Zck,分别将目标变量分为C0,C1,C2,…,Ck类别,其中,C0=(0,Zc1],C1=(Zc1,Zc2],…,Ck=(Zc1,∞]。将每个阈值按照公式(1)对样本值进行指示变换,得到k个指示数据集。
(2)计算指示半变异函数:分别计算每个指示数据集所对应的空间半变异函数,或用中位数作为阈值的半变异函数替代每个等级阈值的半变异函数。
(3)指示克里金插值计算:依次针对阈值Zc1,Zc2,…,Zck,对每一个空间单元使用指示克里金进行空间插值,获得每个空间单元小于第k个阈值的概率P0,P1,P2,…,Pk及其估计误差的标准差sp1,sp2,…,spk。
(4)空间单元等级确定:为每个阈值的概率设置判定的概率阈值Pc1,Pc2,…,Pck,结合上一步计算得到概率估计及其误差对每个空间单元进行类别判定。针对每个空间单元,判定方法如下:
① 针对第i值Zci,计算估计概率的置信区间,[Pi-spi,Pi+spi]。
② 判断空间单元等级:如果i=1,则按照公式(7)对空间单元进行等级划定[16]:
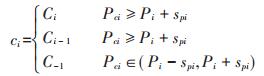
|
(7) |
式中:ci为某等级;Ci为第i级;Ci-1为第i-1级;C-1表示未分等级;Pci为第ci个概率阈值;Pi为第i个概率阈值;spi为第pi个估计误差的标准差。
如果i≠1,按照公式(8)进行等级划定[16]
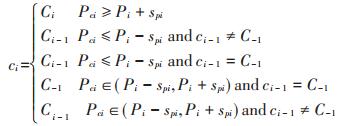
|
(8) |
③ 判断是否已经对所有阈值进行计算,即i是否达到k,若达到,则结束,否则转①继续执行。
(5)划分等级边界:合并同等级空间单元,形成等级边界。
(6)等级划分不确定性分析:通常越是在概率估计值接近概率阈值且估计误差较大处,越容易划错,等级划分的不确定性则越强,等级划分不确定性可以从概率估计值及概率估计误差两方面来确定,并采用错划指数来反映其大小。基于概率阈值进行等级划分,当概率阈值估计误差较小可忽略不计时,概率估计值越接近概率阈值,等级错划概率越大;而概率估计值具有一定的估计误差,特别在一些变异较大且点位稀疏的位置,估计误差通常较大,由此造成的等级划分不确定性也较强。公式(9)计算得到基于概率估计值的错划指数,公式(10)计算得到基于估计误差的错划指数,基于公式(11)获得最终的综合错划指数,其大小反映了等级划分不确定性的强弱。
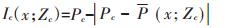
|
(9) |
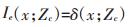
|
(10) |

|
(11) |
式中:Ic(x;Zc)为概率估计值的错划指数;Ie(x;Zc)为概率估计值误差的错划指数;Is(x;Zc)为综合错划指数;Pc为概率阈值;P(x; Zc)为概率估计值;δ(x;Zc)为概率估计值误差。
1.5 等级划分概率阈值的自适应确定方法由上述划分步骤可知,概率阈值Pc对最终等级划分确定结果至关重要。时空指示克里金计算结果为小于阈值的概率,本文中一律采用小于阈值的概率。
在本研究中,通过设定不同的概率阈值来提取基于概率阈值判断的等级划分结果,将划分结果与真实值的等级进行比对,提取不同概率阈值对应的错划指数,最终选择较小错划指数所对应的概率阈值作为最终进行等级划分的概率阈值,从而实现根据研究对象数据特征自适应确定相应的概率阈值。其具体步骤如下:
(1)首先将概率阈值分别设置为0.1、0.2、0.3、…、0.9;在某个概率阈值下,依次保留一个已知样点,采用其他样点基于时空指示克里金对该样点进行等级划分。
(2)将基于时空指示克里金的等级划分结果与真实值的等级进行对比,统计由Juang等[39]提出的第一类错误T1、第二类错误T2、综合错误E。其中第一类错误T1为真实数据未超过阈值而统计推断估计结果将其判断为超过阈值的错误,第二类错误T2为真实数据超过阈值而统计推断估计结果将其判断为未超过阈值的错误。综合错误E即为这两类错误的总和。
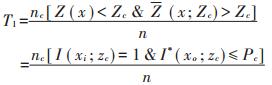
|
(12) |
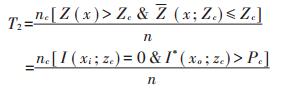
|
(13) |
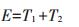
|
(14) |
式中:Zc表示等级阈值;Z(x)表示x位置上的真实值;Z (x; Zc)表示x位置上基于阈值Zc的估计值;n表示研究区域总数据量;I(xi;zc)表示基于阈值的指示值;I*(xo;zc)表示克里金插值概率估计值;Pc为概率阈值。
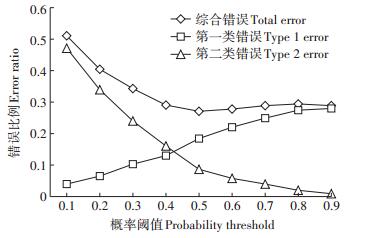
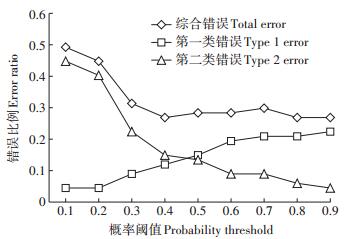
(3)最后绘制等级划分误差图,根据研究对象数据特征和研究需求自适应确定合适的概率阈值。如图 2示例,在等级划分错误比例图中,随着概率阈值的增大,第一类错误增加,第二类错误则会减少。如果需要第一类错误最小,概率阈值选择0.1;如果需要第二类错误最小,概率阈值选择0.9;若需要第一类错误和第二类错误最相近,则概率阈值选择0.5;若需要错划比例最小,则概率阈值选择0.4。
|
图 2 基于概率阈值的等级划分错误比例示例图 Figure 2 The grade classification error ratio diagram based on probability threshold |
根据上述时空指示克里金的等级划分方法以及等级划分概率阈值的自适应确定方法的实现步骤,研究采用Java及R语言,实现了基于时空不确定性分析的农田土壤环境质量等级划分软件。该软件依托于gstat、rgeos、rgdal等R包,并调用vgmST函数和krigeST函数来构建相关的时空半变异函数和时空指示克里金插值计算,对土壤重金属含量进行等级划分和概率阈值的自适应确定。
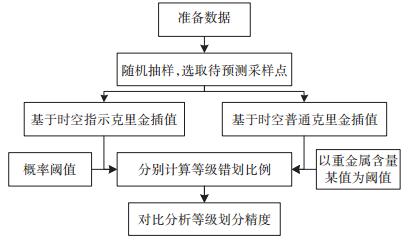
1.6 性能对比分析为了检验基于时空指示克里金的等级划定精度,本研究选择了基于时空普通克里金的等级划分结果与基于时空指示克里金的等级划分结果进行比对。具体的对比流程图如图 3所示,其具体步骤如下:
|
图 3 等级划分性能对比分析流程图 Figure 3 Flow chart of the grade classification comparison analysis |
(1)准备数据。基于研究中所用的北京市土壤重金属含量数据,分别准备一套重金属含量原始值数据和一套基于北京市背景值进行指示变换后的重金属含量指示值数据。
(2)通过随机抽样,确定用于交叉检验的待预测点位。为确保待预测点位的代表性,以2013年数据为基础,随机抽样选取一半样点作为最终的待预测点位。这套点位同时运用于下一步骤中两种方法的插值。
(3)采用两种方法分别进行插值。使用2013年以前的所有年份采样点以及2013年未被选中而剩下的样点作为插值样点,分别基于各自的数据进行时空指示克里金插值和时空普通克里金插值。
(4)统计预测点位的等级错划比例。以上一节确定的概率阈值为最终的概率阈值,基于时空指示克里金插值结果,按照公式(12)、公式(13)、公式(14)计算预测点位的等级错划比例;以北京市土壤重金属的某值为最终的阈值,基于时空普通克里金插值结果,按照公式(12)、公式(13)、公式(14)计算预测点位的等级错划比例。
(5)基于时空指示克里金的等级划定的错划比例结果和基于时空普通克里金的等级划定的错划比例,分析基于时空指示克里金等级划定的性能。
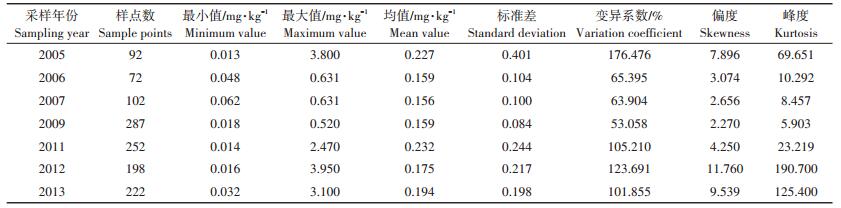
2 结果与讨论 2.1 土壤重金属元素的时空变异分析土壤重金属镉含量的描述性统计结果如表 1所示,2005、2006、2007、2009、2011、2012年和2013年镉含量是不断变化的。其中镉含量的均值在2011年达到最大为0.232 mg·kg-1,在2007年最小0.156 mg·kg-1;变异系数最小值为2009年的53.058%,最大值为2005年的176.476%;偏度最大值为2012年的11.760,最小值为2009年的2.270;峰度最大值为2012年的190.700,最小值为2009年的5.903。
|
|
表 1 土壤重金属镉含量的时空统计特征 Table 1 Spatial-temporal statistics characteristics of soil metal cadmium content |
以陈同斌等[40]研究获得的北京市土壤中重金属镉背景值0.119 mg·kg-1为阈值,将所有年份的样点数据按照公式(1)进行指示变化,小于背景值的赋值为1,大于背景值的赋值为0。对时空指示克里金的时空半变异函数进行了拟合,如图 4所示。其中指示克里金的输入值为镉含量值的指示值。图 4a及图 4b分别为时空指示克里金最终拟合的时空半变异函数的散点图和三维图。

|
图 4 IK的时空半变异函数散点图及三维图 Figure 4 IK spatial-temporal semi-variogram plot and 3D graph |
基于拟合的时空半变异函数进行时空指示克里金插值,得到了最终的土壤重金属镉的概率值。根据等级划分中概率阈值的自适应确定方法,将预测点位的插值结果与其对应的真实值进行比较,分别统计对应的第一类错误、第二类错误和综合错划比例,结果如图 5所示。基于第一类错误与第二类错误的和在概率阈值为0.4的情况下达到最低,且后续趋近平稳,因此本研究中确定最终等级划分的概率阈值为0.4。
|
图 5 概率阈值错误比例统计 Figure 5 Probability threshold error proportion statistic |
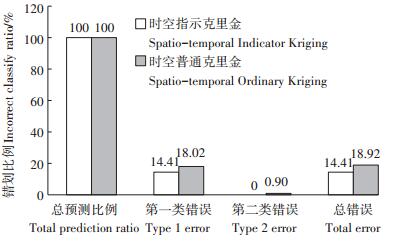
按照1.6节中的性能对比分析步骤,分别计算基于时空指示克里金插值结果和时空普通克里金插值结果的等级划分错划比例,其中时空指示克里金插值结果以2.2节确定的概率阈值0.4为最终的概率阈值,而时空普通克里金插值结果以北京市农田土壤重金属镉的平均土壤背景值0.119 mg·kg-1为最终的阈值。两种插值方法最终统计的错误比例如图 6所示,其中基于时空指示克里金等级划分的综合错误数的错误比例为14.41%,而基于时空普通克里金等级划分的综合错误数的错误比例为18.92%,交叉检验结果表明基于时空指示克里金插值的等级划分的错误数小于基于时空普通指示克里金插值的等级划分所产生的错误数,由此可看出,在对北京市农田土壤重金属镉含量进行等级划分时,相对于时空普通克里金,采用基于时空指示克里金的等级划分方法能取得较高的等级划分精度。
|
图 6 不同方法对应的错误个数 Figure 6 The classification error proportion of IK and OK |
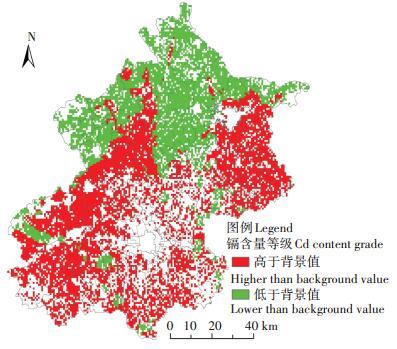
基于时空指示克里金的等级划分确定方法,最终得到了2013年北京市农田土壤重金属镉含量等级分布图以及镉含量等级的错划指数分布图,分别如图 7和图 8所示。图 7反映了研究区土壤重金属镉含量等级的分布情况,镉含量等级分为高于背景值和低于背景值两个级别,红色区域为高于背景值等级,绿色区域为低于背景值区域。图 8反映了镉含量等级的错划指数分布情况,错划指数越大,即错划的可能性较大,说明镉含量的等级划分的不确定性越强;错划指数越小即错划的可能性较小,则说明镉含量等级划分的不确定性越低。
|
图 7 镉含量的等级分布图 Figure 7 The grade distribution map of cadmium content |

|
图 8 镉含量等级的错划指数分布图 Figure 8 The error index distribution map of cadmium content grade |
结合图 7镉含量等级分布图及图 8错划指数分布图分析,在不确定性较低区域,大兴南部地区、昌平部分地区、平谷中部地区、房山南部地区、朝阳区等地的镉含量等级极大可能为高于背景值;延庆大部分地区、怀柔部分地区等地的镉含量等级极大可能为低于背景值;其他区域还需进一步调查确认。其中镉含量等级为大于背景值的区域与蒋红群等[7]预测的镉含量高风险区及中警风险区一致,且与实际情况吻合。根据以往研究[41-43]可知,农田区域镉含量主要是来源于含镉热稳定剂的地膜降解、污水灌溉、采矿活动、大气沉降及其他人类活动。距离城镇中心较近的农田区域,受人类活动影响相对更加强烈,重金属镉更容易累积,因此在大兴南部地区、昌平部分地区、平谷中部地区、房山南部地区、朝阳区等距离城镇中心较近的农田区域,其镉含量等级极大可能为高于背景值;而距离城镇中心较远的农田区域本身成土母质含量低,受人类活动影响较小,重金属镉累积效应较弱,因此在延庆大部分地区、怀柔部分地区等远郊区的农田区域,其镉含量等级极大可能低于背景值。
部分农田区域镉含量等级不确定性较强,其主要原因包括两方面:一方面是受样点分布影响,在点位稀疏区域其估计误差较大,尤其是在变异较大位置;另一方面是受概率阈值影响,基于时空指示克里金插值获取得到的概率估计值越接近概率阈值时,其等级错划概率就越大。这两个因素在镉含量等级不确定性的贡献度方面可依据上述相应公式计算来进一步分析。针对不确定性较强的农田区域,可根据生产生活或监测管理需求进行补充调查,为加密采样提供了指导;或者结合相关辅助数据进一步确认,但是由于时空指示克里金无法利用辅助数据,后续研究将尝试引入协变量对该方法进行改进。
本文基于镉含量背景值利用基于时空指示克里金的等级划分方法对北京市农田土壤重金属镉含量进行了等级划分。根据原农业部印发的“土十条”实施意见,后续可将该方法进一步广泛应用于耕地土壤环境质量类别划分工作中,为农田土壤环境质量科学管理和决策提供支撑。
3 结论(1)研究采用的基于时空指示克里金的等级划分方法,能够利用多期时空采样数据对土壤环境质量进行等级划分,可以自适应确定等级划分的概率阈值,并能估计等级划分的不确定性程度。该方法可为耕地土壤环境质量类别划分工作提供辅助支撑。
(2)北京市2013年农田土壤重金属镉含量的等级分布显示:在昌平大部分地区、平谷中部地区、大兴南部地区、房山南部等距离城镇中心较近区域,其农用地镉含量等级极大可能为高于背景值;而在延庆西部地区、怀柔北部地区等远离城镇中心区域,其农用地的镉含量等级极大可能为低于背景值。
(3)北京市2013年农田土壤重金属镉含量等级错划指数分布反映了北京市农田土壤重金属镉含量等级划分的不确定性程度。其受样点分布及概率阈值确定的影响。
| [1] |
中华人民共和国环境保护部.全国土壤污染状况调查公报[R].北京: 中华人民共和国环境保护部, 2014. The Ministry of Environmental Protection of the People′ s Republic of China. Official journal of national survey on soil pollution[R]. Beijing: The Ministry of Environmental Protection of PRC, 2014. |
| [2] |
中华人民共和国环境保护部, 中华人民共和国农业部.农用地土壤环境管理办法试行[R].北京: 中华人民共和国环境保护部, 中华人民共和国农业部, 2017. The Ministry of Environmental Protection of the People′ s Republic of China, Ministry of Agriculture of the People′ s Republic of China. Methods of soil environmental management for agricultural land(Trial) [R]. Beijing: The Ministry of Environmental Protection of PRC, Ministry of Agriculture of PRC, 2017. |
| [3] |
中华人民共和国国务院.土壤污染防治行动计划[R].北京: 中华人民共和国国务院, 2016. The State Council of the People′ s Republic of China. Action plan on soil pollution control[R]. Beijing: The State Council of PRC, 2016. |
| [4] |
中国国家环境保护局.土壤环境质量标准GB 15618—1995[S].北京: 中国国家环境保护局, 1995. National Environmental Protection Agency of the People ′ s Republic of China. Environmental quality standard for soils GB 15618—1995[S]. Beijing: National Environmental Protection Agency of PRC, 1995. |
| [5] |
中华人民共和国环境保护部.食用农产品产地环境质量评价标准HJ/T 332—2006[S].北京: 中国环境科学出版社, 2006. The Ministry of Environmental Protection of the People′ s Republic of China. Standard of environmental quality assessment for edible agricultural products HJ/T 332—2006[S]. Beijing: China Environmental Science Press. 2006. |
| [6] |
李雪, 李佳桐, 孙宏飞, 等. 琼北农田土壤重金属水平及潜在生态风险[J]. 农业环境科学学报, 2017, 36(11): 2248-2256. LI Xue, LI Jia-tong, SUN Hong-fei, et al. The levels and potential ecological risk of heavy metals in farmland soils in Northern Hainan Province, China[J]. Journal of Agro-Environment Science, 2017, 36(11): 2248-2256. DOI:10.11654/jaes.2017-1022 |
| [7] |
蒋红群, 王彬武, 刘晓娜, 等. 北京市土壤重金属潜在风险预警管理研究[J]. 土壤学报, 2015, 52(4): 731-746. JIANG Hong-qun, WANG Bin-wu, LIU Xiao-na, et al. Early warning of heavy metals potential risk governance in Beijing[J]. Acta Pedologica Sinica, 2015, 52(4): 731-746. |
| [8] |
陆安祥, 孙江, 王纪华, 等. 北京农田土壤重金属年际变化及其特征分析[J]. 中国农业科学, 2011, 44(18): 3778-3789. LU An-xiang, SUN Jiang, WANG Ji-hua, et al. Annual variability and characteristics analysis of heavy metals in agricultural soil of Beijing[J]. Science Agricultural Sinica, 2011, 44(18): 3778-3789. DOI:10.3864/j.issn.0578-1752.2011.18.009 |
| [9] |
孙江, 张国光, 董文光, 等. 北京市农田土壤重金属年际差异分析与评价[J]. 农业环境科学学报, 2011, 30(5): 899-903. SUN Jiang, ZHANG Guo-guang, DONG Wen-guang, et al. Annual variability analysis and evaluation of heavy metals in Beijing agricultural soil, China[J]. Journal of Agro-Environment Science, 2011, 30(5): 899-903. |
| [10] |
霍霄妮, 李红, 张微微, 等. 北京耕作土壤重金属多尺度空间结构[J]. 农业工程学报, 2009, 25(3): 223-229. HUO Xiao-ni, LI Hong, ZHANG Wei-wei, et al. Multi-scale spatial structure of heavy metals in Beijing cultivated soils[J]. Transactions of the CSAE, 2009, 25(3): 223-229. |
| [11] |
Najafian A, Dayani M, Motaghian H R, et al. Geostatistical assessment of the spatial distribution of some chemical properties in calcareous soils[J]. Journal of Integrative Agriculture, 2012, 11(10): 1729-1737. DOI:10.1016/S2095-3119(12)60177-4 |
| [12] |
Goovaerts P. Geostatistics for natural resources evaluation[M]. New York: Oxford University Press, 1997.
|
| [13] |
Isaaks E H, Srivastava R M. An introduction to applied geostatistics[M]. New York: Oxford University Press, 1989.
|
| [14] |
Antunes I M H R, Albuquerque M T D. Using Indicator Kriging for the evaluation of arsenic potential contamination in an abandoned mining area(Portugal)[J]. Science of the Total Environment, 2013, 442(15): 545-552. |
| [15] |
Gao B B, Liu Y, Pan Y C, et al. Error index for additional sampling to map soil contaminant grades[J]. Ecological Indicators, 2017, 77: 129-138. DOI:10.1016/j.ecolind.2017.02.011 |
| [16] |
Gao B B, Lu A X, Pan Y C, et al. Additional sampling layout optimization method for environmental quality grade classifications of farmland soil[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(12): 5350-5358. DOI:10.1109/JSTARS.2017.2753467 |
| [17] |
王彬武, 李红, 蒋红群, 等. 北京市耕地土壤重金属时空变化特征初步研究[J]. 农业环境科学学报, 2014, 33(7): 1335-1344. WANG Bin-wu, LI Hong, JIANG Hong-qun, et al. Spatial-temporal variation of soil heavy metals in agricultural land in Beijing, China[J]. Journal of Agro-Environment Science, 2014, 33(7): 1335-1344. |
| [18] |
安婧, 宫晓双, 陈宏伟, 等. 沈抚灌区农田土壤重金属污染时空变化特征及生态健康风险评价[J]. 农业环境科学学报, 2016, 35(1): 37-44. AN Jing, GONG Xiao-shuang, CHEN Hong-wei, et al. Temporal and spatial characteristics and health risk assessments of heavy metal pollution in soils of Shenfu irrigation area[J]. Journal of Agro-Environment Science, 2016, 35(1): 37-44. |
| [19] |
张静, 邹滨, 陈思萱, 等. 土壤重金属污染风险时空变化模拟与分析[J]. 测绘科学, 2016, 41(10): 88-92. ZHANG Jing, ZOU Bin, CHEN Si-xuan, et al. Spatial-temporal simulation and analysis of health risks of heavy metal contaminated soil[J]. Science of Surveying and Mapping, 2016, 41(10): 88-92. |
| [20] |
杨勇, 梅杨, 张楚天, 等. 基于时空克里格的土壤重金属时空建模与预测[J]. 农业工程学报, 2014, 30(21): 249-255. YANG Yong, MEI Yang, ZHANG Chu-tian, et al. Spatio-temporal modeling and prediction of soil heavy metal based on spatio-temporal Kriging[J]. Transactions of the CSAE, 2014, 30(21): 249-255. DOI:10.3969/j.issn.1002-6819.2014.21.030 |
| [21] |
宋波, 杨子杰, 张云霞, 等. 广西西江流域土壤镉含量特征及风险评估[J]. 环境科学, 2018, 39(4): 1888-1900. SONG Bo, YANG Zi-jie, ZHANG Yun-xia, et al. Accumulation of Cd and its risks in the soils of the Xijiang River drainage basin in Guangxi[J]. Environmental Science, 2018, 39(4): 1888-1900. |
| [22] |
姜菲菲, 孙丹峰, 李红, 等. 北京市农业土壤重金属污染环境风险等级评价[J]. 农业工程学报, 2011, 27(8): 330-337. JIANG Fei-fei, SUN Dan-feng, LI Hong, et al. Risk grade assessment for farmland pollution of heavy metals in Beijing[J]. Transactions of the CSAE, 2011, 27(8): 330-337. DOI:10.3969/j.issn.1002-6819.2011.08.058 |
| [23] |
尹国庆, 江宏, 王强, 等. 安徽省典型区农用地土壤重金属污染成因及特征分析[J]. 农业环境科学学报, 2018, 37(1): 96-104. YIN Guo-qing, JIANG Hong, WANG Qiang, et al. Analysis of the sources and characteristics of heavy metals in farmland soil from a typical district in Anhui Province[J]. Journal of Agro-Environment Science, 2018, 37(1): 96-104. |
| [24] |
肖斌, 赵鹏大, 侯景儒. 时空域中的指示克立格理论研究[J]. 地质与勘探, 1999, 35(4): 25-28. XIAO Bin, ZHAO Peng-da, HOU Jing-ru. The theory of indicator Kriging study in temporal-spatial domain[J]. Geology and Prospecting, 1999, 35(4): 25-28. |
| [25] |
Christakos G. Random field models in earth sciences[M]. San Diego: Academic Press, 1992.
|
| [26] |
Ma C S. Families of spatio-temporal stationary covariance models[J]. Journal of Statistical Planning and Inference, 2003, 116(2): 489-501. DOI:10.1016/S0378-3758(02)00353-1 |
| [27] |
Dimitrakopoulos R, Luo X. Geostatistics for the next century[M]. Netherlands: Kluwer Academic Publishers, 1994: 88-93.
|
| [28] |
Myers D E, Journel A. Variograms with zonal anisotropies and noninvertible kriging systems[J]. Mathematical Geology, 1990, 22(7): 779-785. DOI:10.1007/BF00890662 |
| [29] |
Cressie N, Huang H C. Classes of nonseparable, spatio-temporal stationary covariance functions[J]. Journal of the American Statistical Association, 1999, 94(448): 1330-1340. DOI:10.1080/01621459.1999.10473885 |
| [30] |
Iaco S D, Myers D E, Posa D. Space-time analysis using a general product-sum model[J]. Statistics & Probability Letters, 2001, 52(1): 21-28. |
| [31] |
Iaco S D, Myers D E, Posa D. Nonseparable space-time covariance models: Some parametric families[J]. Mathematical Geology, 2002, 34(1): 23-42. |
| [32] |
Bhunia G S, Kesari S, Chatterjee N, et al. Spatial and temporal variation and hotspot detection of kala-azar disease in Vaishali district(Bihar), India[J]. BMC Infectious Disease, 2013, 13(1): 64. DOI:10.1186/1471-2334-13-64 |
| [33] |
Heuvlink G B M, Griffith D A. Space-time geostatistics for geography: A case study of radiation monitoring across parts of Germany[J]. Geographical Analysis, 2010, 42(2): 161-179. DOI:10.1111/j.1538-4632.2010.00788.x |
| [34] |
Zafra M S, Rado M B, Tobíasat A, et al. Space-time interpolation of daily air temperatures[J]. Journal of Environmental Statistics, 2012, 3(5): 1-15. |
| [35] |
李莎, 舒红, 徐正全. 利用时空Kriging进行气温插值研究[J]. 武汉大学学报(信息科学版), 2012, 37(2): 237-241. LI Sha, SHU Hong, XU Zheng-quan. Interpolation of temperature based on spatial-temporal Kriging[J]. Geomatics and Information Science of Wuhan University, 2012, 37(2): 237-241. |
| [36] |
Griffith D A, Heuvelink G B M. Deriving space-time variograms from space-time autogressive (STAR) model specifications[M]//Griffith D A, Heuvelink G B, Anthony G O, et al. Advances in spatial data handling and GIS: The 14th international symposium on spatial data handling. Berlin: Springer-Verlag, 2012, 38: 3-12.
|
| [37] |
高秉博.时空非平稳区域多目标抽样优化方法[D].北京: 中国科学院大学, 2015. GAO Bing-bo, Multi-targets sampling optimizaiton method for a spatio-temporal non-stationary region[D]. Beijing: The University of Chinese Academy of Sciences, 2015. |
| [38] |
Bilonick R A. Monthly hydrogen ion deposition maps for the northeastern U. S from July 1982 to September 1984[J]. Atmospheric Environment, 1988, 22(9): 1909-1924. DOI:10.1016/0004-6981(88)90080-7 |
| [39] |
Juang K W, Liao W J, Liu T L, et al. Additional sampling based on regulation threshold and kriging variance to reduce the probability of false delineation in a contaminated site[J]. Science of the Total Environment, 2008, 389(1): 20-28. |
| [40] |
陈同斌, 郑袁明, 陈煌, 等. 北京市土壤重金属含量背景值的系统研究[J]. 环境科学, 2004, 25(1): 117-122. CHEN Tong-bin, ZHENG Yuan-ming, CHEN Huang, et al. Background concentrations of soil heavy metals in Beijing[J]. Environmental Science, 2004, 25(1): 117-122. |
| [41] |
Luo L, Ma Y B, Zhang S Z. An inventory of trace element inputs to agricultural soils in China[J]. Journal of Environmental Management, 2009, 90(8): 2524-2530. DOI:10.1016/j.jenvman.2009.01.011 |
| [42] |
成世才, 王兵, 郭加朋, 等. 山东省鱼台水稻生产基地土壤镉分布现状及来源分析研究[J]. 科技情报开发与经济, 2009, 19(31): 130-133. CHENG Shi-cai, WANG Bing, GUO Jia-peng, et al. Soil Cd current distribution and origin study of Yutai rice production base[J]. SCITech Information Development & Economy, 2009, 19(31): 130-133. DOI:10.3969/j.issn.1005-6033.2009.31.063 |
| [43] |
霍霄妮, 李红, 孙丹峰, 等. 北京耕地土壤重金属空间自回归模型及影响因素[J]. 农业工程学报, 2010, 26(5): 78-82. HUO Xiao-ni, LI Hong, SUN Dan-feng, et al. Spatial autogression model for heavy metals in cultivated soils of Beijing[J]. Transactions of the CSAE, 2010, 26(5): 78-82. |
 2019, Vol. 38
2019, Vol. 38